時間積分スキーム SPOOK

• AGXの時間積分にはSPOOKを採用

• 構造保存数値解法のうちのシンプレクティック(Symplectic)解法

• アルゴリズムによる発散や散逸がおきない

• 高周期の振動を安定に計算できる [2]

• 時間積分は1次精度である

• 可変タイムステップは不可

SPOOKとは

時間積分スキームにはオイラー法やルンゲクッタ法などがあるが、AGXは「SPOOK」 [Lacoursière2007] [Lacoursière2011] [Sundling2016] を採用している。 SPOOKは離散力学(Discrete Mechanics)に基づいたシンプレクティック(Symplectic)解法である。 保存系において、エネルギーが一定の範囲に保たれ、アルゴリズムによる発散や散逸がおきない。 また、高周期の振動を安定に計算できる特徴がある。

マルチボディダイナミクスの運動は運動方程式(微分方程式)と拘束条件式(代数方程式)を連立した微分代数方程式(DAE、Differential Algebraic Equations)として表される。 例えば、運動方程式とホロノミック拘束は次のようになる [3] 。

(1)\[\begin{split}\begin{aligned} & \bm{M} \ddot{\bm{q}} = \bm{f} + \bm{G}^T \bm{\lambda} & \rm{(a)} \\ & \epsilon_i \bm{\lambda} + g_i(\bm{q}) + \tau_i \dot{g}_i(\bm{q})=0 & \rm{(b)} \end{aligned}\end{split}\]

ここで、

\(\bm{q}\) : 一般化座標	\(\dot{\bm{q}}\) : 一般化速度
\(\ddot{\bm{q}}\) : 一般化加速度	\(g(\bm{q})\) : ホロノミック拘束条件関数
\(\bm{G}=\frac{\partial g}{\partial q}\) : ヤコビ行列 [1]	\(\bm{f}\) : 外力ベクトル
\(\bm{\lambda}\) : ラグランジュ定数ベクトル	\(\epsilon\) : コンプライアンス
\(\tau\) : スプークダンパ

である。式(1) をSPOOKの形式で時間離散化すると、

速度の更新

(2)\[\begin{split}\left[\begin{array}{cc} \bm{M} & -\bm{G}_k^T \\ \bm{G}_k & \bm{\Sigma} \end{array}\right]\left[\begin{array}{c} \bm{v}_{k+1} \\ \bm{\lambda_{k+1}} \end{array}\right]=\left[\begin{array}{c} \bm{M} \bm{v}_k+h \bm{f}_k \\ -\frac{4}{h} \bm{\gamma} \bm{g}_k+\bm{\gamma} \bm{G}_k \bm{v}_k \end{array}\right]\end{split}\]

位置の更新

(3)\[\bm{x}_{k+1} = \bm{x}_k + h \bm{v}_{k+1}\]

となる。ただし、

\(k\) : 計算ステップ数	\(\bm{\Sigma} = \frac{4}{h^2}\rm{diag}[\frac{\epsilon_i}{1 + 4 \tau_i / h}]\)
\(\bm{\gamma} = \rm{diag}[\frac{1}{1 + 4 \tau_i / h}]\)	\(\bm{v}\) : 速度
\(\bm{x}\) : 位置	\(h\) : タイムステップ

である。 AGXは 式(2) について、ソルバで \(\bm{v_{k+1}}\) と \(\bm{\lambda_{k+1}}\) を求め、 式(3) で位置の更新をする。

精度は1次精度

数値解と真解との差は \(O(h)\) であり、はタイムステップの大きさに比例する。 拘束条件がない場合、速度と位置の更新はSemi implicitオイラースキームと同じになる。

(4)\[\begin{split}\begin{aligned} \bm{v}_{k+1} &= \bm{v}_{k} + h \bm{M}^{-1} \bm{f}_k \\ \bm{x}_{k+1} &= \bm{x}_{k} + h \bm{v}_{k+1} \\ \end{aligned}\end{split}\]

可変タイムステップは不可

固定タイムステップで構造保存が成立するスキームとなっている。

例: 減衰振動

理解を深めるために、重力を無視した減衰振動の運動をSPOOKで記述する。 減衰振動の運動方程式は

\(m\) : 質点の質量

\(x\) : 位置

\(v\) : 速度

\(k\) : ばね係数(弾性係数)

\(c\) : 減衰係数

として、

(5)\[m \dot{v} = -kx - cv\]

である。ここで、\(g(x) = x\) として、質点を0の位置に拘束すると、\(G = {\partial g}/{\partial x} = 1\) となることから、 式(1) のDAEの形式で記述すると、

(6)\[\begin{split}\begin{aligned} & m \dot{v} = \lambda & \rm{(a)} \\ & \lambda = -kx - cv & \rm{(b)} \end{aligned}\end{split}\]

となる。拘束条件 式(6) (b)を変形し、式(1) との対応を取ると、

(7)\[\frac{1}{k} \lambda + x + \frac{c}{k}v = 0\]

となり、コンプライアンス、スプークダンパ、ばね係数、減衰係数の関係が得られる。

(8)\[\epsilon = \frac{1}{k}, \tau = \frac{c}{k}\]

式(6) をSPOOKのスキームで離散化すると、速度の更新は

(9)\[\begin{split}\left[\begin{array}{cc} m & -1 \\ 1 & \frac{4 \gamma \epsilon}{h^2} \end{array}\right]\left[\begin{array}{c} v_{k+1} \\ \lambda_{k+1} \end{array}\right]=\left[\begin{array}{c} m v_k \\ -\frac{4}{h} \gamma x_k + \gamma v_k \end{array}\right]\end{split}\]

となる。ただし、\(\gamma = \frac{1}{1+4 \tau / h}\) 。 これは2変数2本の連立方程式なので、\(v_{k+1}\) と \(\lambda_{k+1}\) について解ける ( 導出 )。

(10)\[\begin{split}\begin{aligned} & v_{k+1} = \frac{-\frac{4}{h} \gamma x_k + \gamma v_k + \frac{4 \gamma \epsilon m}{h^2} v_k}{1 + \frac{4 \gamma \epsilon m}{h^2}} \\ & \lambda_{k+1}=m v_{k+1}-m v_k \end{aligned}\end{split}\]

上式の \(v_{k+1}\) を 式(3) に代入し、位置の更新をする。

単振動シミュレーションによるSPOOKの安定性の確認

確認内容と条件

単振動 \(m \dot{v} = -kx\) を対象に次のスキームでシミュレーションし、SPOOKの安定性の確認をした。

• Analytical: 解析解

• SPOOK

• Explicit Euler: 前進オイラー

• Implicit Euler: 後退オイラー

• Semi Implicit Euler: シンプレクティックオイラー

初期条件とタイムステップを次に示す。

\(m\)	1kg
\(x_0\)	1m
\(v_0\)	0m/s
\(h\)	0.0167s

単振動 \(k = 100 \rm{\,N/m}\)

条件を \(k = 100 \rm{\,N/m}\) とした結果を 図 2 と 図 3 、 図 4 に示す。

図 2 より前進オイラーは時間の進行とともに振幅が大きくなり、発散し、「不安定」である。 したがって、保存系のシミュレーションの使用には不適である。

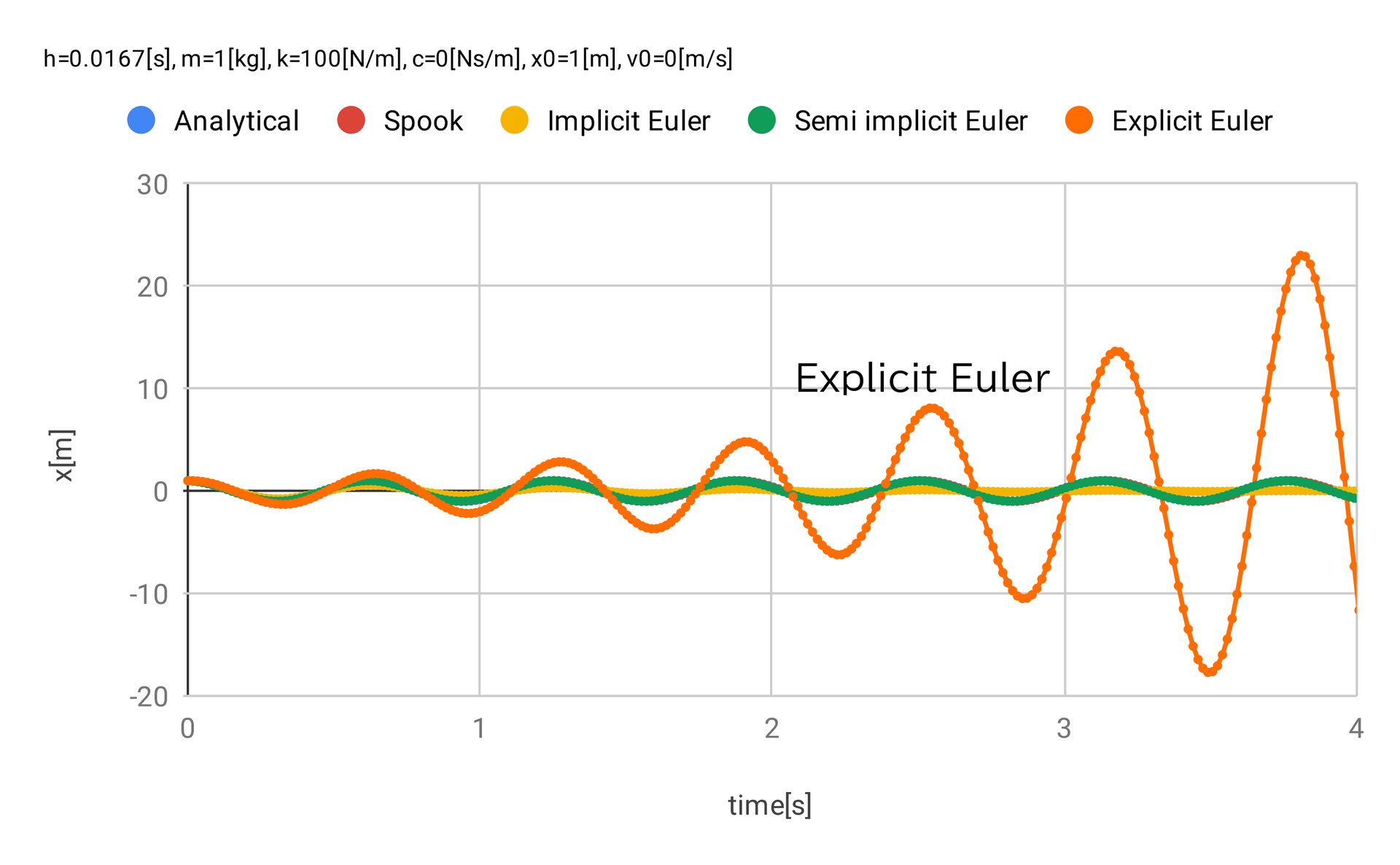
図 2 単振動 \(k = 100 \rm{\,N/m}\)

図 3 は 図 2 のExplicit Eulerを除外し、振幅1mの範囲で拡大したものである。 後退オイラーは時間の進行とともに減衰し、収束していることから「漸近安定」である。 後退オイラーも振動の波形の再現ができておらず、保存系のシミュレーションの使用には不適である。 SPOOKとシンプレクティックオイラーは発散も収束もせず、解析解に追従している。

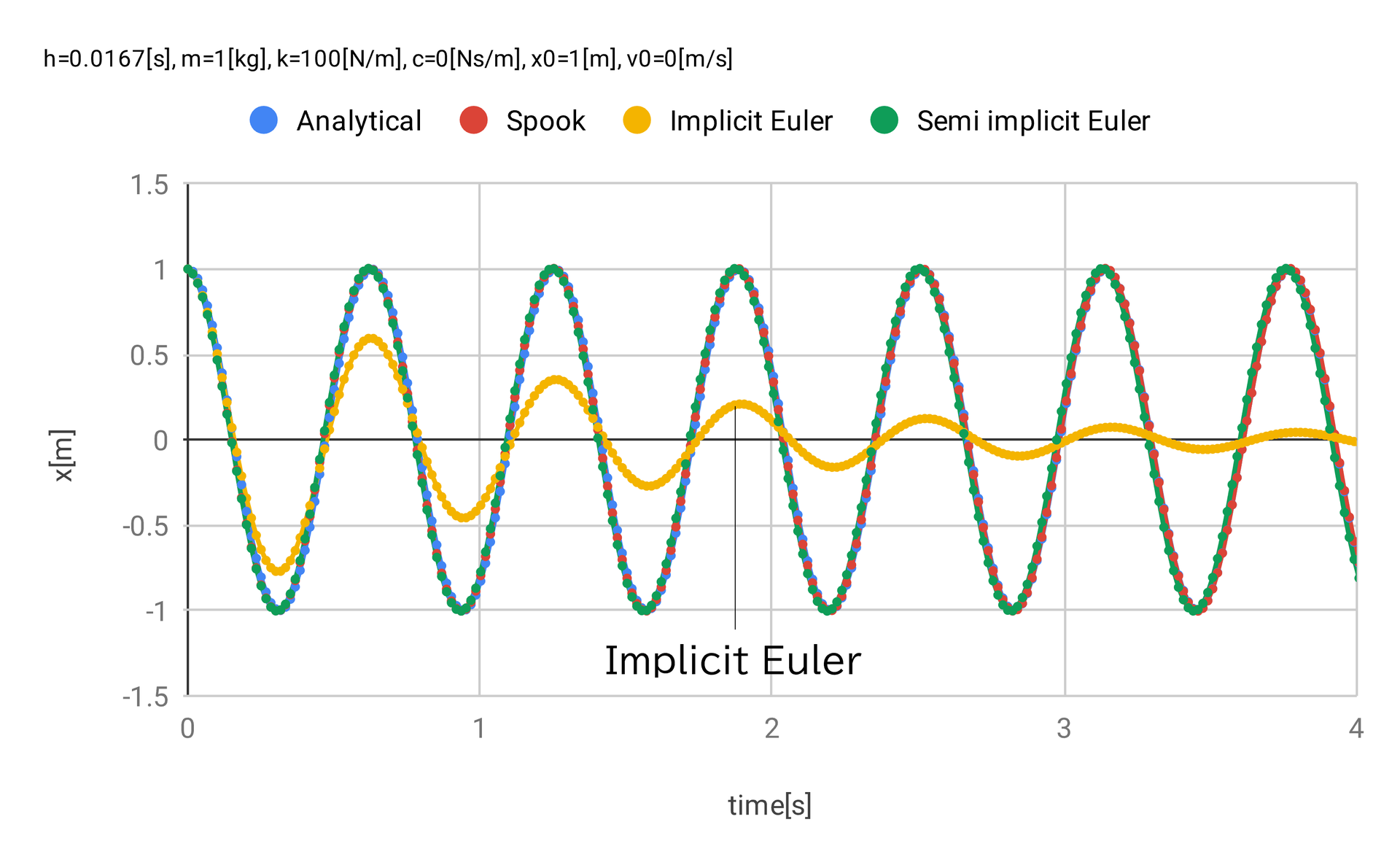
図 3 単振動 \(k = 100 \rm{\,N/m}\) 拡大版

系のエネルギー( 図 4 )について確認すると、 SPOOKとシンプレクティックオイラーは一定の範囲でゆらいで(振動して)いて、エネルギーを厳密に保存していない。

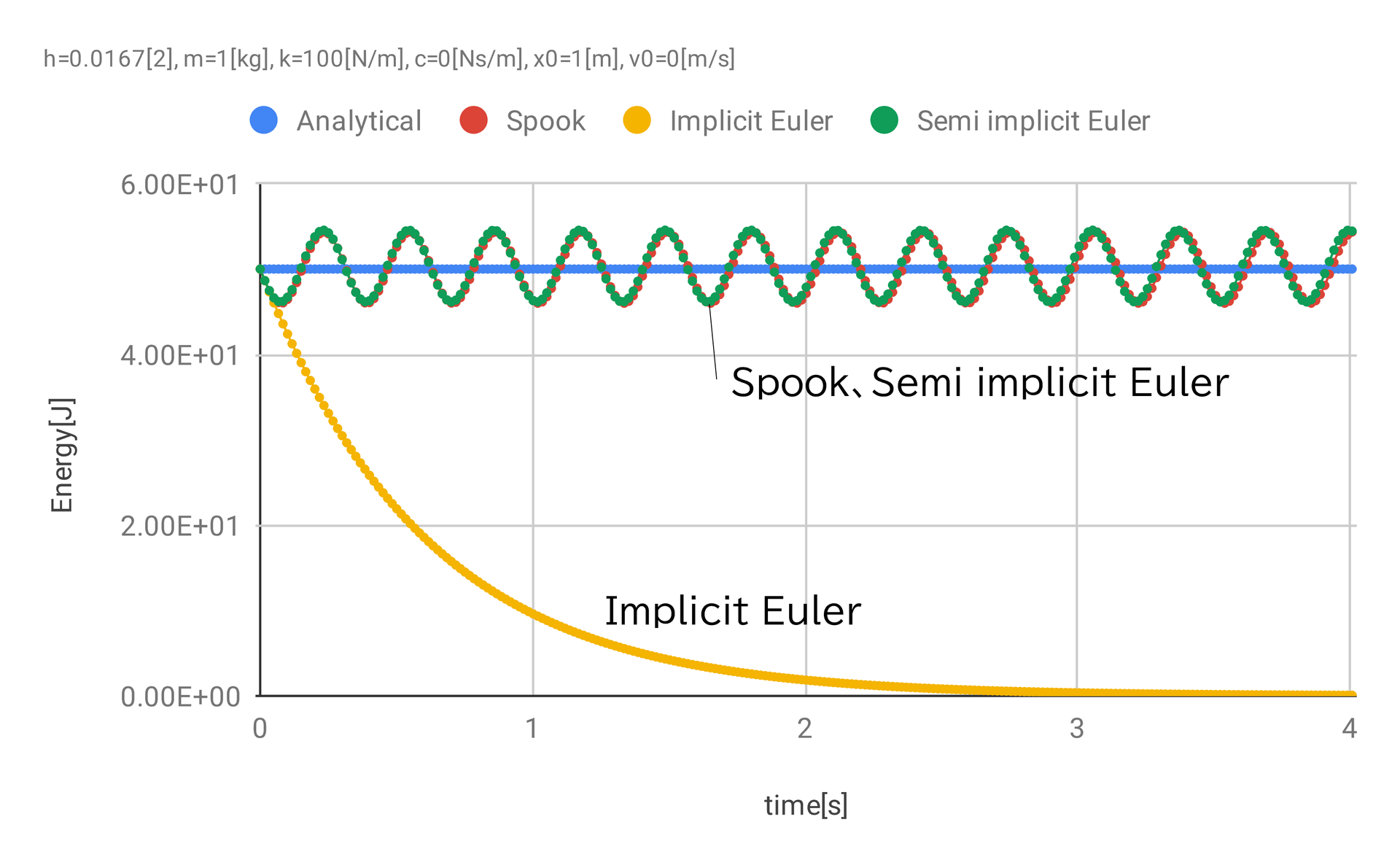
図 4 単振動 \(k = 100 \rm{\,N/m}\) のエネルギー

単振動 \(k = 4m/h^2\) : シンプレクティックオイラーの安定限界

シンプレクティックオイラーは「条件付き安定」であり、安定条件は \(k \le 4m/h^2\) である。 これを基準に \(k = 4m/h^2 \pm 1 \approx 1.434e4 \pm 1 \rm{\,N/m}\) として、シミュレーションをした。 結果を 図 5 と 図 6 、 図 7 に示す。

図 5 は \(k\) の値をシンプレクティックオイラーの安定条件内とした場合の結果である。 シンプレクティックオイラーは振幅が100mを超え、波形を正しく再現できていない。 しかし、発散も収束もしておらず、「安定」 [2] である。

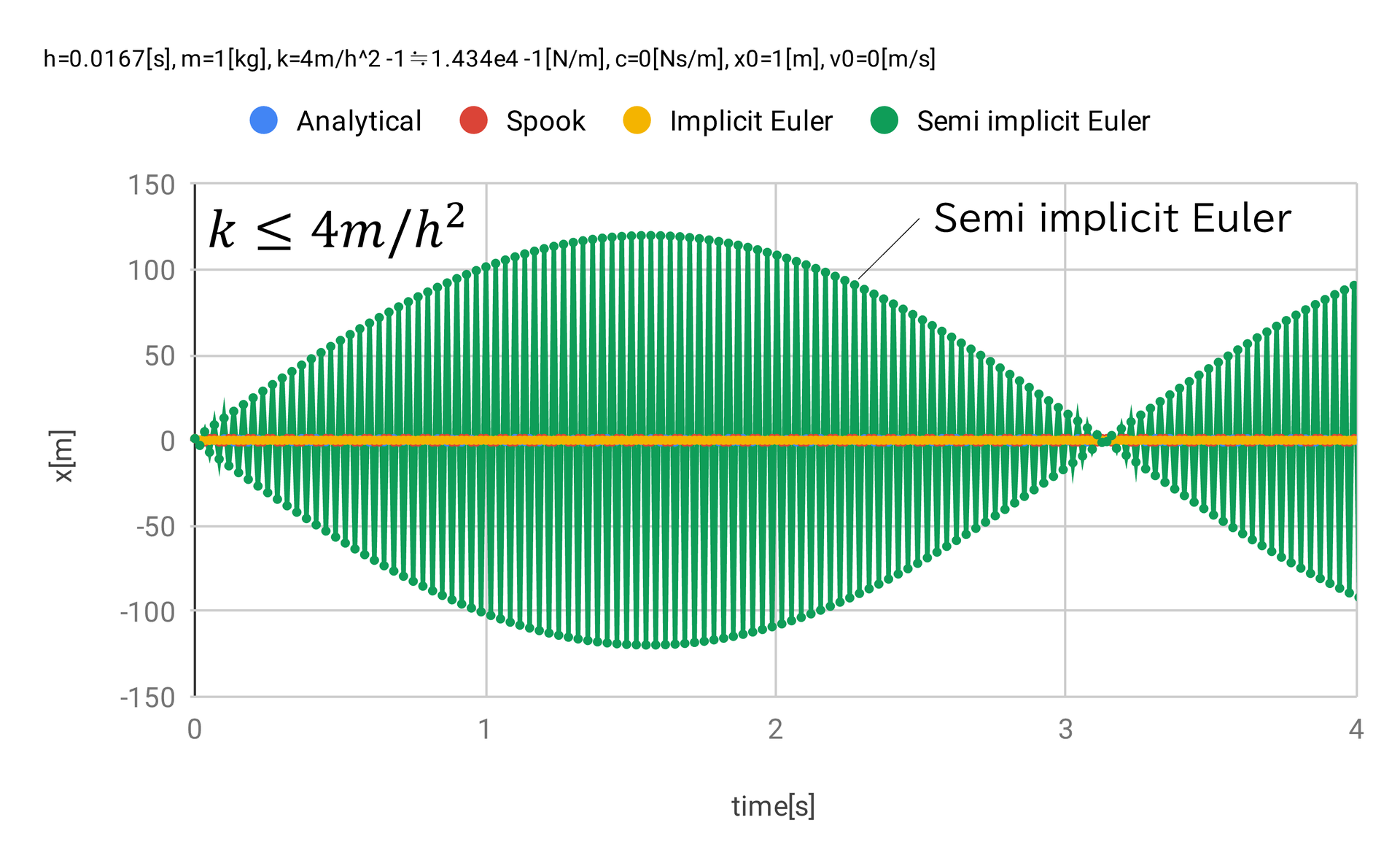
図 5 単振動 \(k = 4m/h^2 - 1\)

図 6 は \(k\) の値をシンプレクティックオイラーの安定条件外とした場合の結果である。 シンプレクティックオイラーの波形は発散しており、「不安定」である。

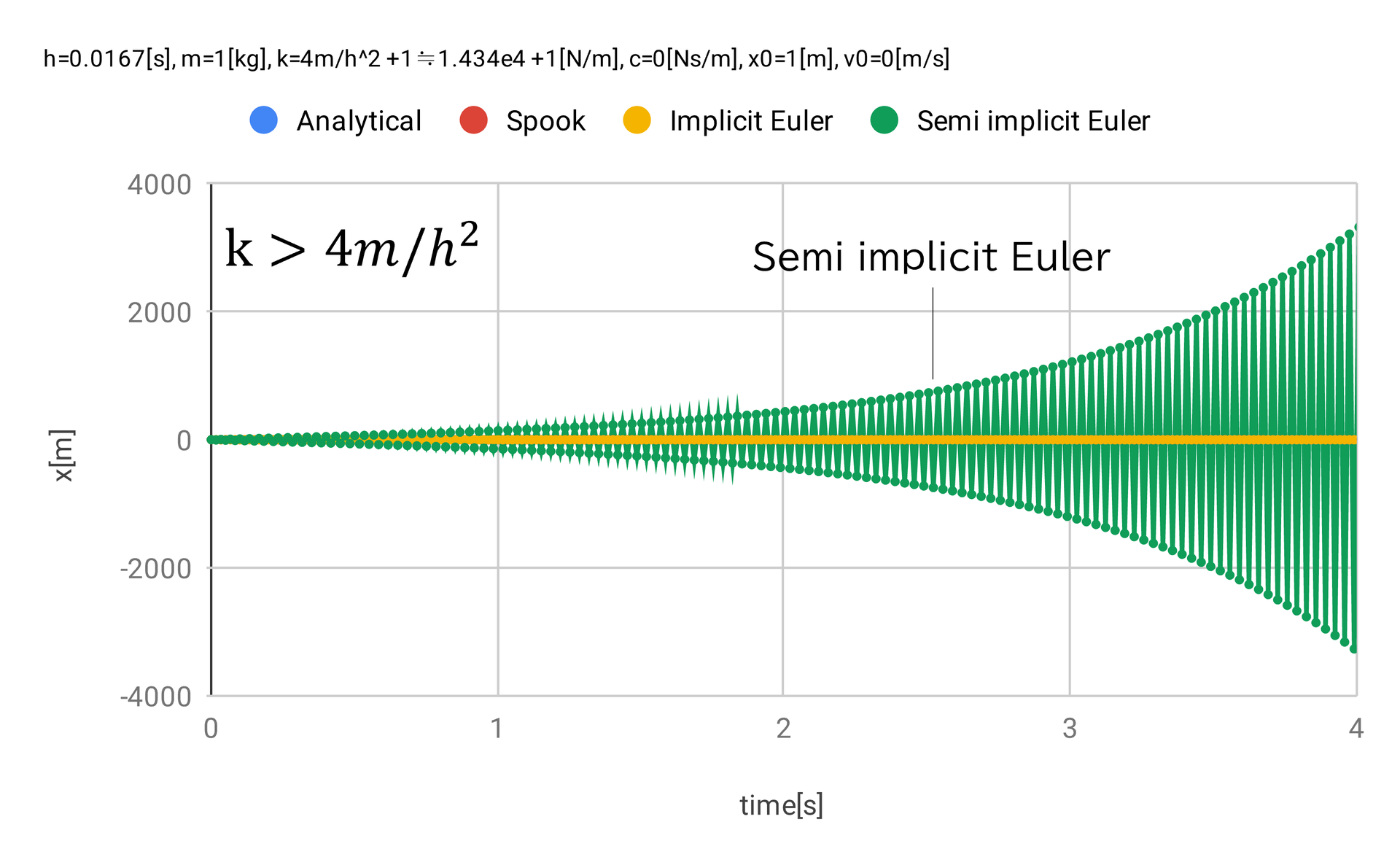
図 6 単振動 \(k = 4m/h^2 + 1\)

図 7 は 図 6 の振幅について-1から1mの範囲で拡大したものである。 タイムステップが大きいため、解析解とSPOOKともに滑らかな波形ではない(タイムステップを小さくすれば滑らかな波形になる)。 また、振動周期の理論値は \(T = 0.0524 \rm{\,s}\) であるが、SPOOKは異なっており、位相がずれている。 SPOOKは発散しておらず、「安定」である。

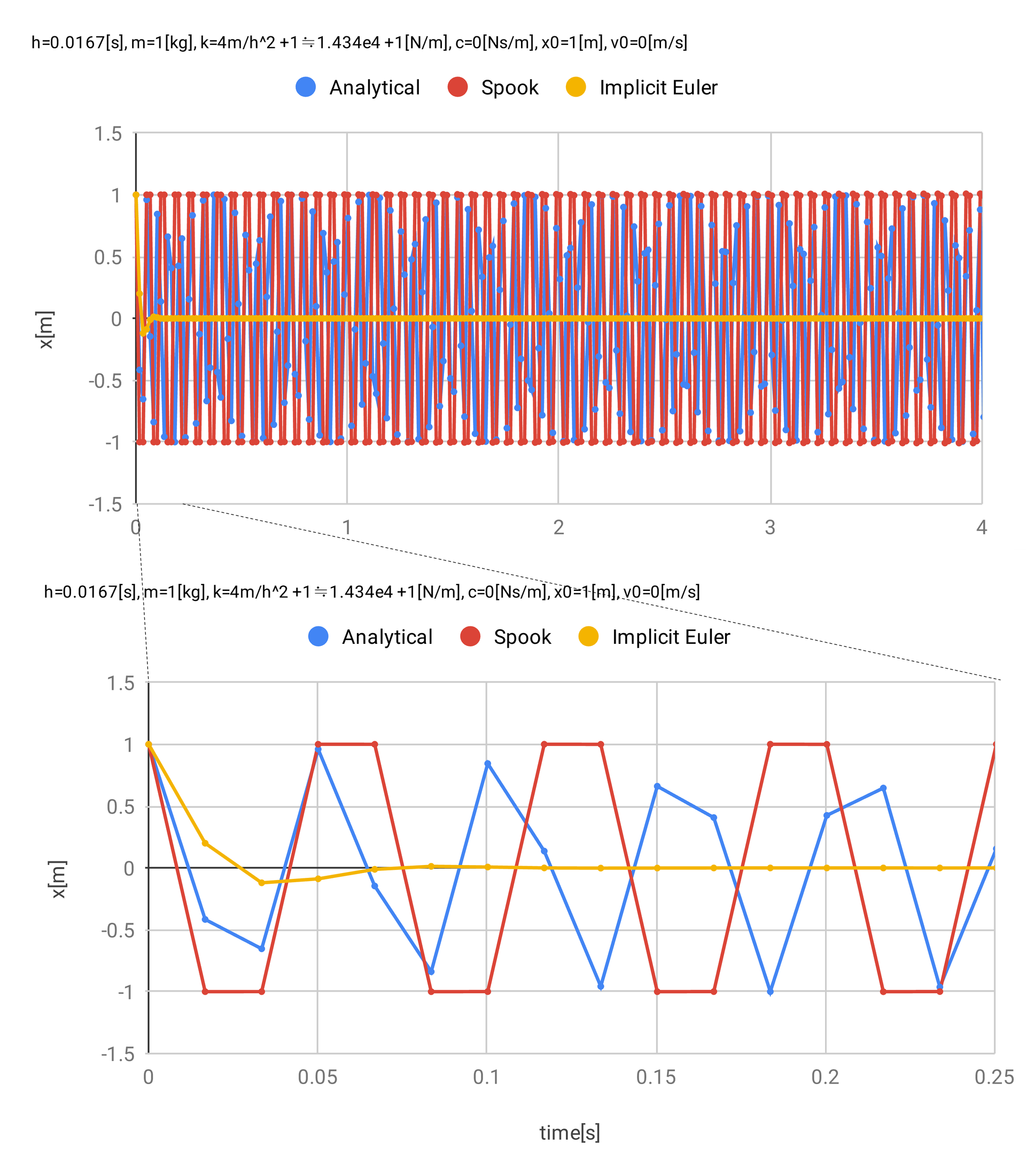
図 7 単振動 \(k = 4m/h^2 - 1\) 拡大版

単振動 \(k = 4m \pi^2/h^2\) 、 \(k=\infty\)

さらに \(k\) を大きくしていき、SPOOKの安定性を探る。 \(k\) を次の値についてシミュレーションした結果を 図 8 と 図 9 示す。

\(k = 4m \pi^2/h^2 \approx 1.42 \times 10^5 \rm{\,N/m}\)

\(k=\infty \rm{\,N/m}\)

図 8 の振動周期の理論値は \(T = 0.0167 \rm{\,s}\) で、 タイムステップと同じである。 解析解はサンプリングのタイミングが常に \(\theta = 0 \rm{\,rad}\) の時になるので、直線となる。 振動波形が再現できておらず、「エイリアシング」が発生している。 Spookもサンプリングが不足しており、振幅が大きくなっているが、発散しておらず「安定」である。

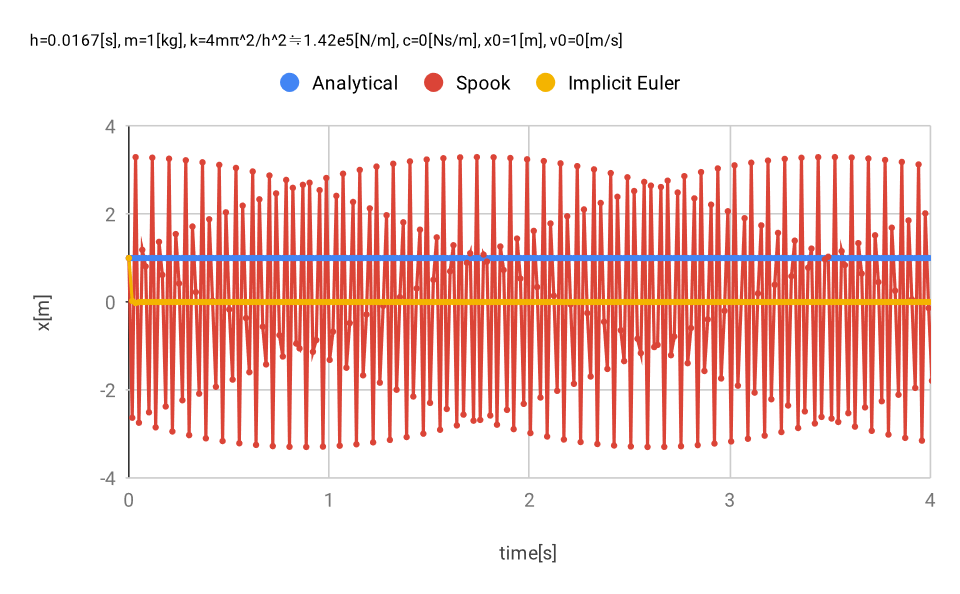
図 8 単振動 \(k = 4m \pi^2/h^2\)

図 9 はSPOOKのみを表示している。 図 8 と同様に波形の再現はできていないが、発散しておらず「安定」である。

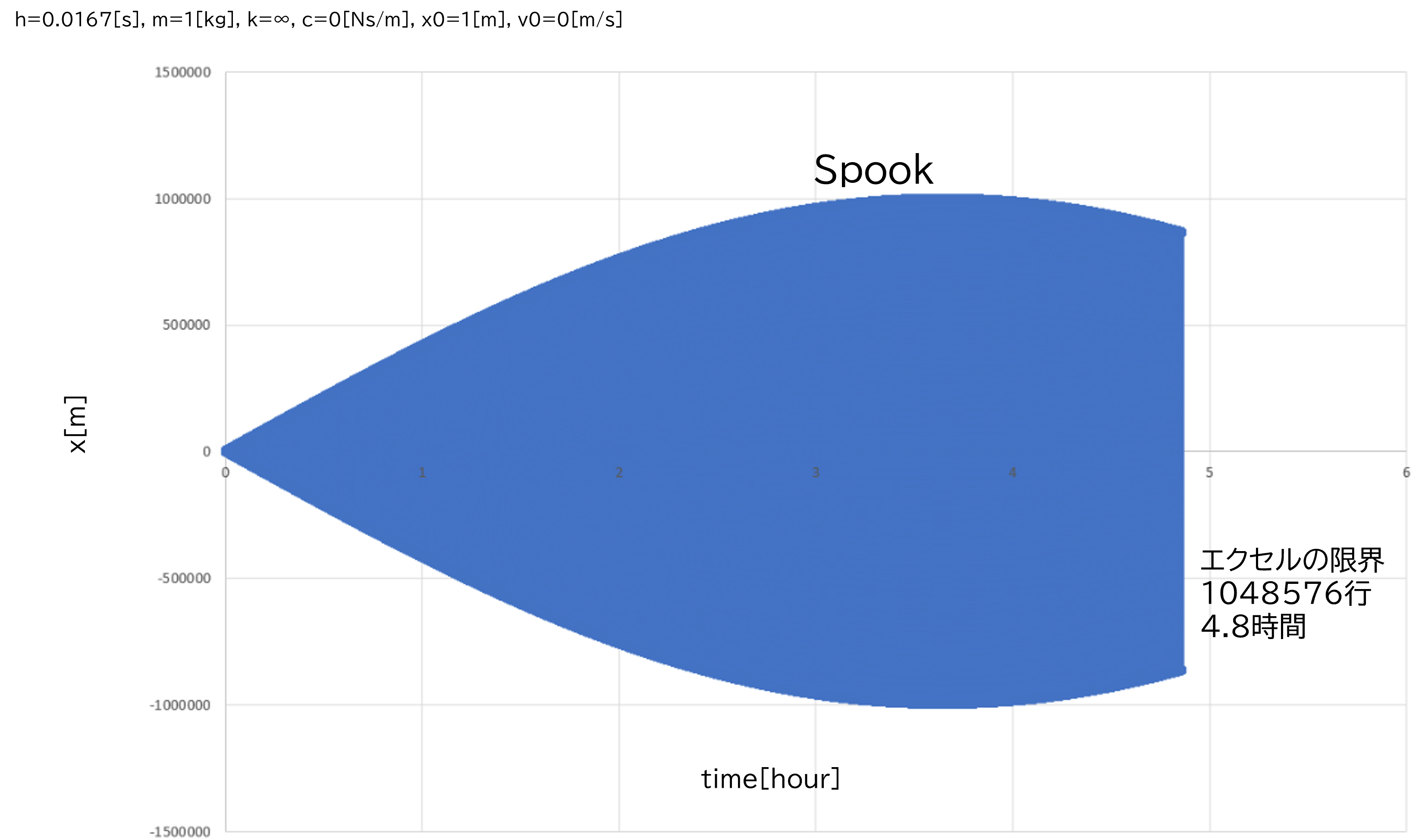
図 9 単振動 \(k=\infty\)

参考文献

[Lacoursière2007]

Claude Lacoursière. Ghosts and Machines: Regularized Variational Methods for Interactive Simulations of Multibodies with Dry Frictional Contacts. PhD thesis, Department of Computing Science, Umea University, Sweden, SE-901 87, Umea, Sweden, June 2007, URL: https://umu.diva-portal.org/smash/record.jsf?pid=diva2%3A140361&dswid=1753.

[Lacoursière2011] (1,2)

Claude Lacoursière and Mattias Linde. Spook: a variational time-stepping scheme for rigid multibody systems subject to dry frictional contacts. Technical report, HPC2N and Department of Computing Science, Umea University, Sweden, 2011, URL: https://webapps.cs.umu.se/uminf/index.cgi?year=2011&number=9.

[Sundling2016]

Emma Sundling. Validation toolbox for a Physics Engine. Master thesis, Physics Department, Umea University, Sweden, 2016, URL: https://umu.diva-portal.org/smash/record.jsf?pid=diva2%3A935814&dswid=8436.

補足

式(9) から 式(10) の導出

式(9) を展開すると、

(11)\[\begin{split}\begin{aligned} & m v_{k+1}-\lambda_{k+1}=m v_k & \rm{(a)} \\ & v_{k+1}+\frac{4 \gamma \epsilon}{h^2} \lambda_{k+1}=-\frac{4}{h} \gamma x_k+\gamma v_k & \rm{(b)} \end{aligned}\end{split}\]

となる。(a)を \(\lambda_{k+1}=m v_{k+1}-m v_k\) に変形し、(b)に代入し、整理すると \(v_{k+1}\) が得られる。

(12)\[\begin{split}\begin{aligned} & v_{k+1} + \frac{4 \gamma \epsilon}{h^2} (m v_{k+1} - m v_k) = -\frac{4}{h} \gamma x_k + \gamma v_k \\ & v_{k+1} + \frac{4 \gamma \epsilon m}{h^2} v_{k+1} - \frac{4 \gamma \epsilon m}{h^2} v_k = -\frac{4}{h} \gamma x_k + \gamma v_k \\ & v_{k+1} \left( 1 + \frac{4 \gamma \epsilon m}{h^2} \right) = -\frac{4}{h} \gamma x_k + \gamma v_k + \frac{4 \gamma \epsilon m}{h^2} v_k \\ & v_{k+1} = \frac{-\frac{4}{h} \gamma x_k + \gamma v_k + \frac{4 \gamma \epsilon m}{h^2} v_k}{1 + \frac{4 \gamma \epsilon m}{h^2}} \end{aligned}\end{split}\]

(a)に \(v_{k+1}\) 代入し、整理すると、\(\lambda_{k+1}\) が得られる。

(13)\[\lambda_{k+1} = m \left( \frac{-\frac{4}{h} \gamma x_k + \gamma v_k + \frac{4 \gamma \epsilon m}{h^2} v_k}{1 + \frac{4 \gamma \epsilon m}{h^2}} \right) - m v_k\]

[1]

ロボット工学ではヤコビアン。

(14)\[\dot{g}(q) = \frac{d}{dt}g(\bm{q}) = \frac{\partial g}{\partial q} \frac{d q}{d t} = \bm{G} \dot{\bm{q}}\]

[2] (1,2)

安定は「妥当」でも「正確」でもない。安定だからといって「安心」はできない。

[3]

実際は非ホロノミック拘束、接触拘束も含めて扱う。例えば、 [Lacoursière2011] を参照のこと。