agxTerrainの土質力学

• agxTerrainが扱う連続体の土質力学について説明する。

土の構成

土質力学における土の構成は水分を考慮しているが、 agxTerrainは土の質量保存を成立させるため、水分を無視している。

• 間隙水はなし

• 圧密排水による土の質量変化はなし

  • 土工作業中に排水による土の質量変化はないと仮定

これにより、土の構成 [菊本2015] は

\(m_\mathrm{a} \approx 0\) : 空気の質量	\(m_\mathrm{w} \approx 0\) : 水の質量	\(m_\mathrm{s}\) : 土粒子の質量
\(V_\mathrm{a}\) : 空気の体積	\(V_\mathrm{w} \approx 0\) : 水の体積	\(V_\mathrm{s}\) : 土粒子の体積
\(\rho_\mathrm{a} = \frac{m_\mathrm{a}}{V_\mathrm{a}}\) : 空気の密度	\(\rho_\mathrm{w} = \frac{m_\mathrm{w}}{V_\mathrm{w}}\) : 水の密度	\(\rho_\mathrm{s} = \frac{m_\mathrm{s}}{V_\mathrm{s}}\) : 土粒子の密度

として、次式で表される。

土密度(soil density)

(17)\[\begin{aligned} \rho &= \frac{\cancel{m_\mathrm{a}} + \cancel{m_\mathrm{w}} + m_\mathrm{s}}{V_\mathrm{a} + \cancel{V_\mathrm{w}} + V_\mathrm{s}} = \frac{m_\mathrm{s}}{V_\mathrm{a} + V_\mathrm{s}} = \frac{m_\mathrm{s}}{V} \end{aligned}\]

間隙比(void ratio)

(18)\[\begin{aligned} e &= \frac{V_\mathrm{a} + \cancel{V_\mathrm{w}}}{V_\mathrm{s}} = \frac{V_\mathrm{a}}{V_\mathrm{s}} \end{aligned}\]

比体積(specific volume)

(19)\[\begin{aligned} e + 1 &= \frac{V_\mathrm{a}}{V_\mathrm{s}} + 1 = \frac{V_\mathrm{a} + V_\mathrm{s}}{V_\mathrm{s}} = \frac{V}{V_\mathrm{s}} = \frac{\cancel{m_\mathrm{s}}}{\rho}\frac{\rho_\mathrm{s}}{\cancel{m_\mathrm{s}}} = \frac{\rho_\mathrm{s}}{\rho} \end{aligned}\]

体積分率(volume fraction)

(20)\[\begin{aligned} \varphi &= (e + 1)^{-1} = \frac{V_\mathrm{s}}{V} = \frac{\rho}{\rho_\mathrm{s}} \end{aligned}\]

土の圧縮

土に荷重をかけたり、ほぐしたりすると、土粒子の位置や間隙の変化により、土の体積が変化する。 体積の変化に伴い、土の密度や硬さが変化し、土への貫入・分離抵抗力の大きさに影響する。 agxTerrainはこれらの過程を次の流れで計算する。

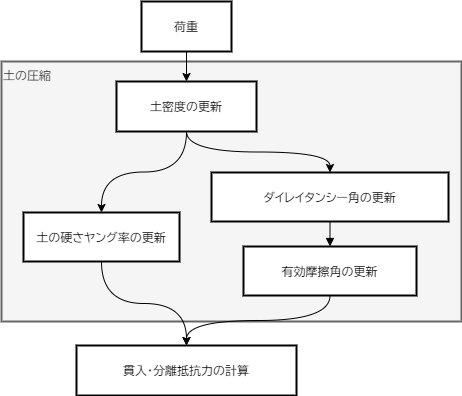
土密度の更新

• Soil Compaction — AGX Dynamics documentation

土は圧縮されると空気が抜け、密度が大きくなる。 agxTerrainは圧縮指数(compression index)を使い土密度を更新する。

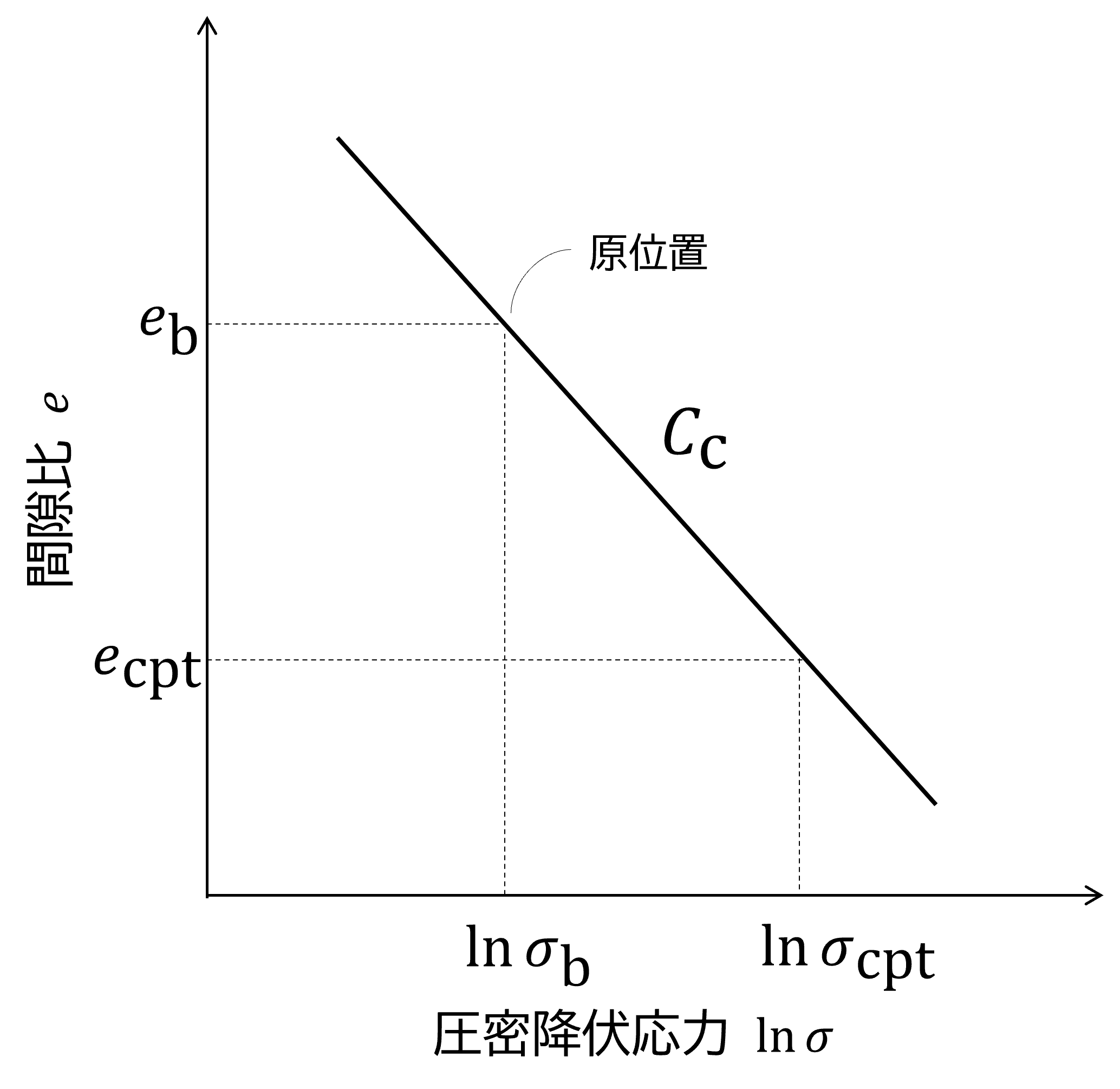
図 11 圧縮曲線(\(e \text{-} \log p\) 曲線)

ここで、

\(\rho_\mathrm{b}\) : 原位置の土密度 [2]	\(\rho_\mathrm{s}\) : 土粒子密度
\(\varphi_\mathrm{b} = \rho_\mathrm{b} / \rho_\mathrm{s}\) : 原位置の体積分率 [2]
\(e_\mathrm{b} = \rho_\mathrm{s} / \rho_\mathrm{b} - 1\): 原位置の間隙比	\(e_{\mathrm{cpt}} = \rho_\mathrm{s} / \rho_{\mathrm{cpt}} - 1\) : 圧縮後の間隙比
\(\sigma_b\) : 先行圧密応力 [2]	\(\sigma_{\mathrm{cpt}}\) : 圧縮後の応力

とおく。圧縮指数 \(C_\mathrm{c}\) [2] は

(21)\[\begin{aligned} C_\mathrm{c} &= \frac{e_\mathrm{b} - e_{\mathrm{cpt}}}{\ln(\sigma_{\mathrm{cpt}}/\sigma_b)} \end{aligned}\]

である [1] 。 式(21) から応力 \(\sigma_{k+1}\) のときの土密度 \(\rho_{k+1}\) を 導出 すると、

(22)\[\begin{split}\begin{aligned} \rho_{k+1} &= \rho_\mathrm{b} \left[ 1 - \varphi_\mathrm{b} C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_b} \right) \right]^{-1} \\ \end{aligned}\end{split}\]

となる。応力 \(\sigma_{k+1}\) 以外は定数であるので、応力から土密度 \(\rho_{k+1}\) が得られる。

土の硬さヤング率の更新

• Young's Modulus — AGX Dynamics documentation

土の硬さはヤング率で表す。 土は圧縮されると硬くなり、ヤング率が大きくなる。

\(E_\mathrm{b}^{\mathrm{bulk}}\) : 原位置のヤング率 [2]	\(E_{k+1}^{\mathrm{bulk}}\) : 更新後のヤング率
\(k_\mathrm{E}\) : 比例硬化定数 [2]	\(n_\mathrm{E}\) : 指数硬化定数 [2]

とおいて、agxTerrainは土密度 \(\rho_{k+1}\) のときのヤング率 \(E_{k+1}^{\mathrm{bulk}}\) を

(23)\[\begin{aligned} E_{k+1}^{\mathrm{bulk}} = E_\mathrm{b}^{\mathrm{bulk}} \left( 1.0 \pm k_\mathrm{E} \left| \frac{\rho_{k+1}}{\rho_\mathrm{b}} - 1.0 \right| \right)^{n_\mathrm{E}} \end{aligned}\]

と表す。 土密度 \(\rho_{k+1}\) 以外は定数であるので、土密度からヤング率 \(E_{k+1}^{\mathrm{bulk}}\) が得られる。

\(k_E\) と \(n_E\) は粒子の充填構造を表すパラメータである。 これはHertz接触モデルを使い、粒子の配置状態とヤング率の関係から導出されたものである [agxTerrainReport2019] 。 理想的な配置で粒子が充填されている状態は \(k_E = 1.0\) と \(n_E = 0.5\) である。 参考として、\(E_\mathrm{b}^{\mathrm{bulk}} = 0.5\mathrm{e}7\) 、\(\rho_\mathrm{b} = 1300\) として、 それぞれのパラメータ値を変化させたときの振る舞いを下図に示す。

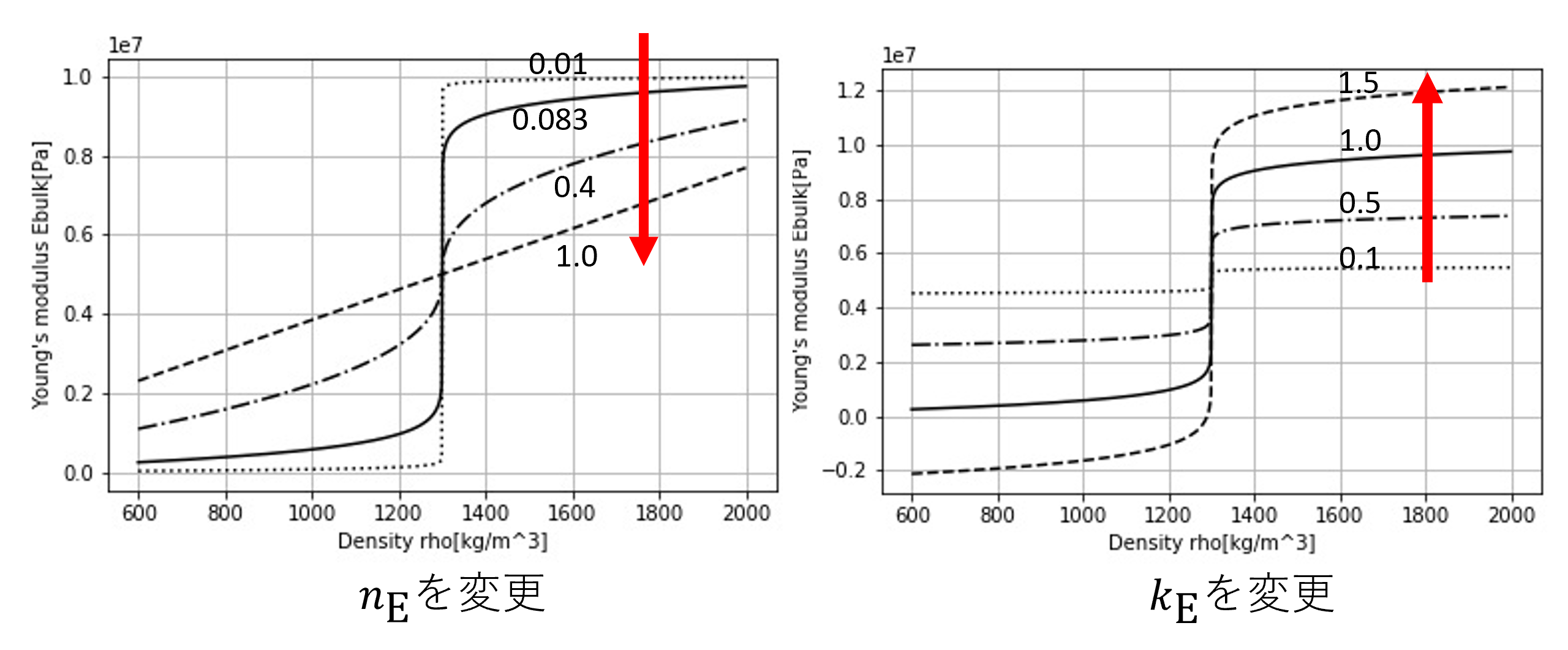
図 12 土密度とヤング率の関係

ダイレイタンシー角の更新

• Dilatancy Angle — AGX Dynamics documentation

土が圧縮され密に詰まった状態でせん断変形すると、土の体積が膨張する。 せん断変形に伴う体積膨張をダイレイタンシー(dilatancy)とよぶ。

図 13 砂のダイレイタンシー特性 ( [菊本2015] より引用)

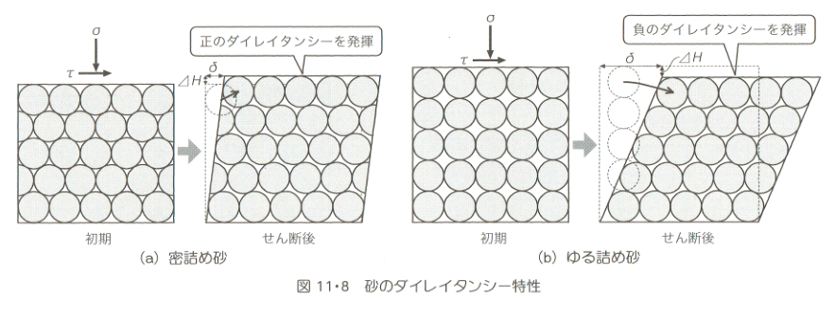
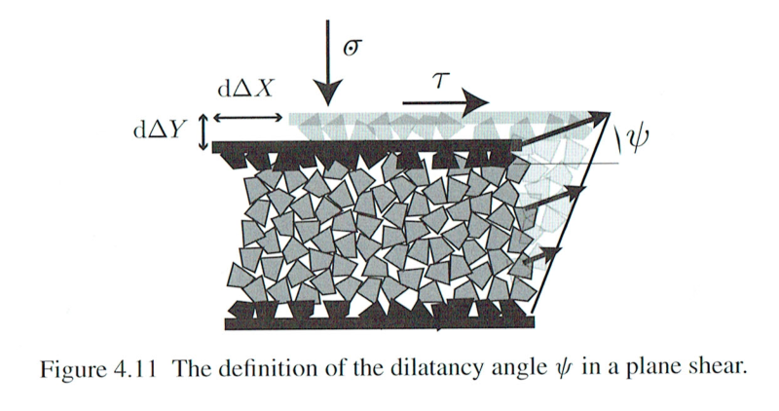
図 14 ダイレイタンシー角 ( [Andreotti2013] より引用)

ダイレイタンシーによるせん断変形量 \(\Delta X\) と高さの変形量 \(\Delta Y\) とで成す角を ダイレイタンシー角(dilatancy angle) \(\psi\) とよぶ [Andreotti2013] 。

(24)\[\begin{split}\begin{aligned} \frac{d \Delta Y}{d \Delta X} &= \tan \psi \\ \psi &= \arctan \frac{d \Delta Y}{d \Delta X} \end{aligned}\end{split}\]

\(\psi > 0\) のときは正のダイレイタンシーとよび、密詰めの土の体積が膨張していることを示す。 \(\psi < 0\) のときは負のダイレイタンシーとよび、ゆる詰めの土の体積が圧縮していることを示す。

密詰めの土のせん断はゆる詰めに比べて大きなせん断力が必要である。 agxTerrainではダイレイタンシー角と摩擦角(せん断力)を関連付けて、ダイレイタンシーによるせん断力への影響を反映させる。 関連付けについては 次のセクション で説明する。

ダイレイタンシー角を定義通りに求めることは難しいため、agxTerrainは [Roux1998] ( [Andreotti2013] で紹介) が提案している土密度とダイレイタンシー角の関係式を使う。

ここで、

\(\varphi_{k+1}\) : 最新の体積分率	\(\varphi_\mathrm{c}\) : 限界状態の体積分率
\(\psi_\mathrm{b}\) : 原位置のダイレイタンシー角 [2]	\(c_\rho = \psi_\mathrm{b} \left( \frac{\rho_\mathrm{b}}{\rho_\mathrm{b} - \rho_\mathrm{c}} \right)\) : 定数

とおいて、土密度 \(\rho_{k+1}\) とダイレイタンシー角 \(\psi_{k+1}\) の関係式は

(25)\[\begin{aligned} \psi_{k+1} &= c_\rho \left( \frac{\rho_{k+1}}{\rho_\mathrm{b}} - \frac{\rho_\mathrm{c}}{\rho_\mathrm{b}} \right) \end{aligned}\]

である。土密度 \(\rho_{k+1}\) 以外は定数であり、土密度から更新後のダイレイタンシー角 \(\psi_{k+1}\) が得られる。

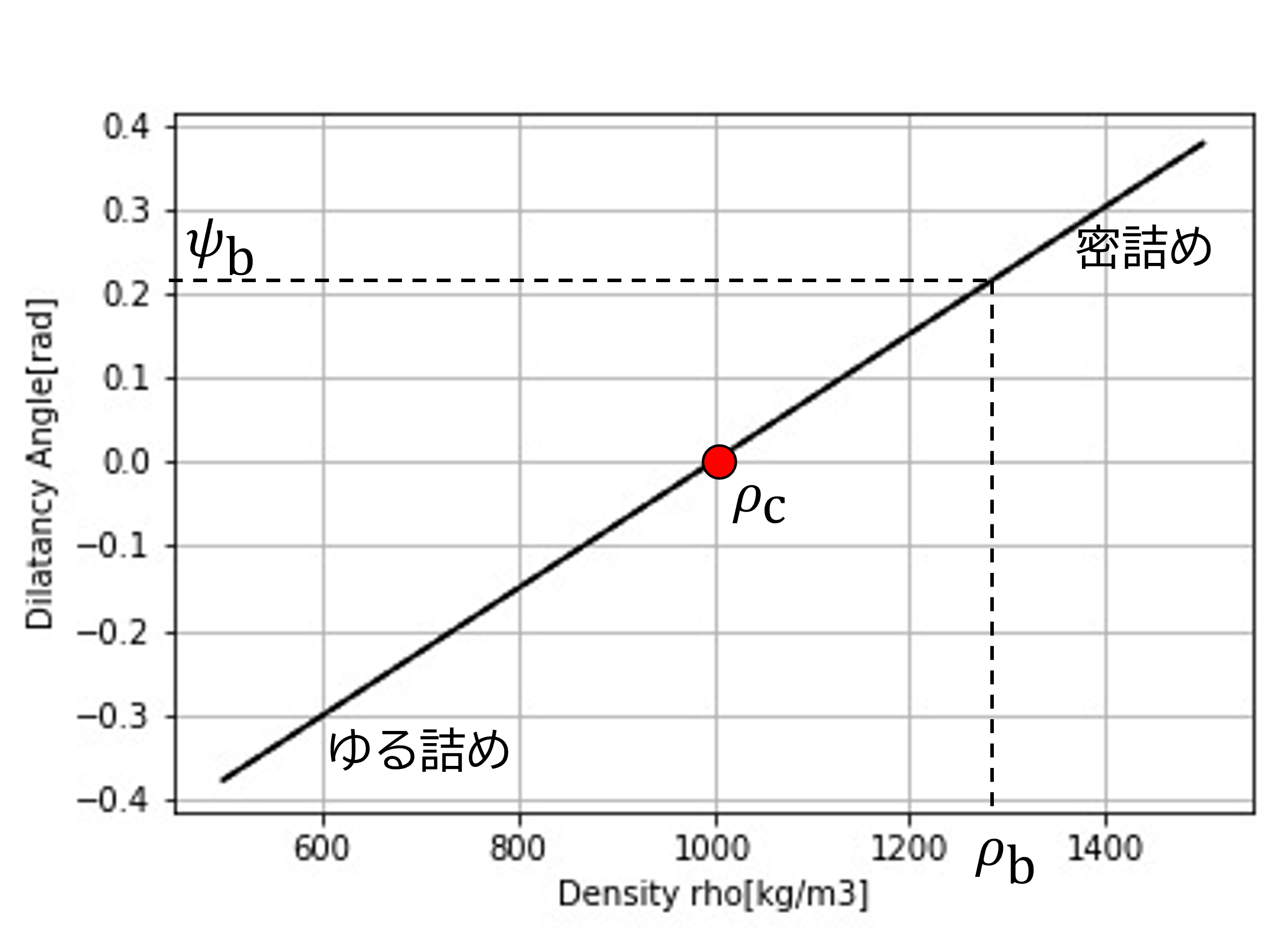
例として、式(25) を図示する。 臨界状態の密度 \(\rho_\mathrm{c}\) を境に、密詰め(正のダイレイタンシー)、ゆる詰め(負のダイレイタンシー)となる。

有効摩擦角の更新

• Dilatancy Angle — AGX Dynamics documentation

agxTerrainではダイレイタンシーの影響を含む内部摩擦角を有効内部摩擦角(effective internal friction angle)とよぶ。 前セクション のダイレイタンシー角 \(\psi_{k+1}\) を使い、有効内部摩擦角を更新する。

\(\phi_\mathrm{b}\) : 原位置の内部摩擦角 [2]

とおいて、有効内部摩擦角 \(\phi_{k+1}\) は

(26)\[\begin{aligned} \phi_{k+1} = \phi_\mathrm{b} + \psi_{k+1} \end{aligned}\]

である。

土ほぐしによる土量と密度の更新

• Swelling — AGX Dynamics documentation

地山を切崩したり掘削をすると、土がほぐされ、空気が含まれることで土の体積(土量)が増加する。 agxTerrainではこの現象を土量変化率(swell factor)を使い、土の体積と密度を更新することで表現する。

\(V_k\) : 更新後の土量	\(V_k^\mathrm{before}\) : 更新前の土量
\(\rho_{k}\) : 更新後の土密度	\(\rho_{k}^\mathrm{before}\) : 更新前の土密度

とおくと、土量変化率 \(S_\mathrm{f}\) [2] は

(27)\[\begin{aligned} S_\mathrm{f} = \frac{\mathrm{ほぐした土量}}{\mathrm{地山土量}} = \frac{V_k}{V_k^\mathrm{before}} = \frac{\rho_{k}^\mathrm{before}}{\rho_{k}} \end{aligned}\]

である。 ほぐした後の体積と密度はそれぞれ、

(28)\[\begin{split}\begin{aligned} V_{k} &= S_\mathrm{f} V_k^\mathrm{before} \\ \rho_{k} &= \frac{1}{S_\mathrm{f}} \rho_{k}^\mathrm{before} \end{aligned}\end{split}\]

となる。 例えば、図 15 のSoil 20%の場合、 \(S_\mathrm{f} = 1.2\) であるので、 \(V_{k} = 1.2 V_k^\mathrm{before}\) 、 \(\rho_{k} = 0.83 \rho_{k}^\mathrm{before}\) となる。

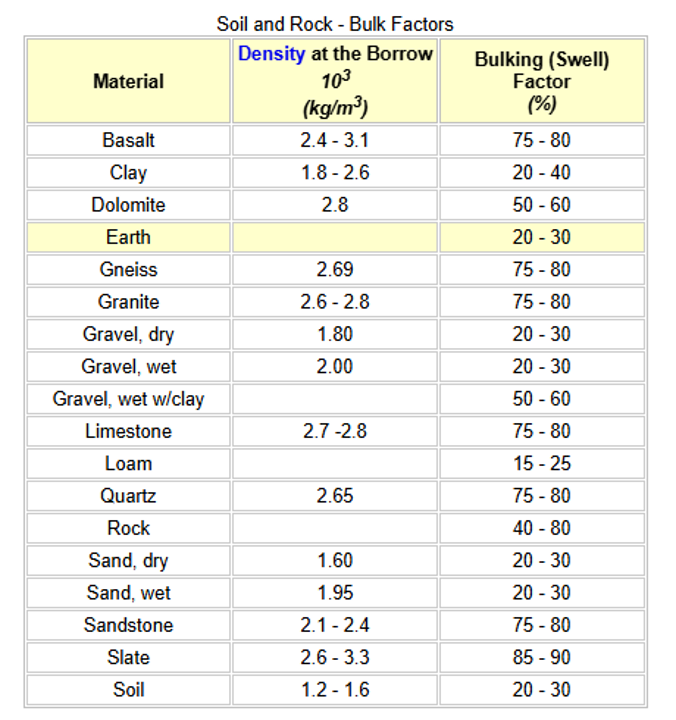
図 15 Swell factor ( [EngineeringToolBox2009] より引用)

ショベルの貫入抵抗力の計算

• Penetration Resistance Model — AGX Dynamics documentation

ショベルの貫入抵抗力(penetration resistance force)の計算には、 土質特性とショベルに加わる土圧に基づいた [Bennett2016] [Park2002] のモデルを使う。

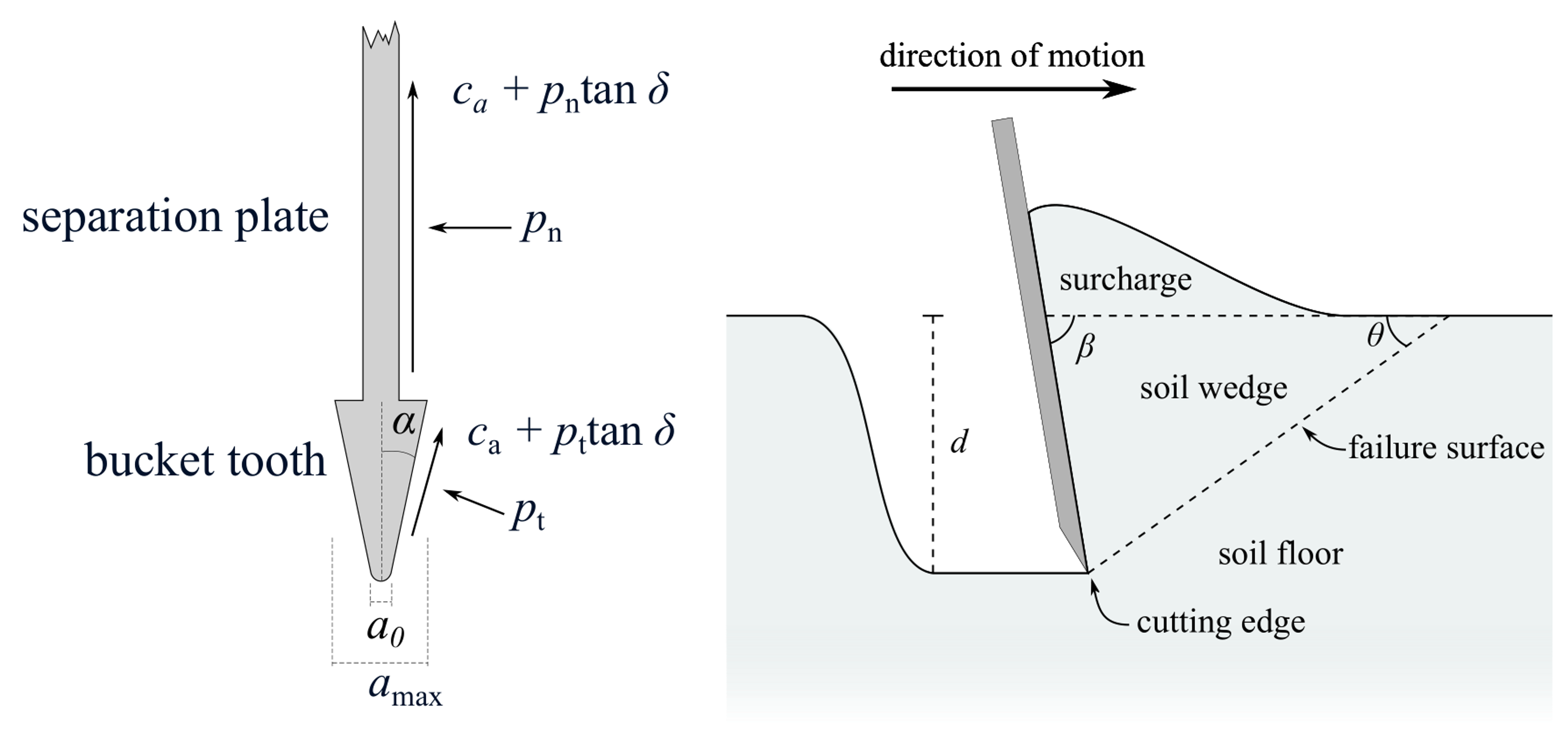
ここで、

\(a_0\) : 歯の先端直径 [2]	\(a_\mathrm{max}\) : 歯の根本直径 [2]
\(l_\mathrm{t}\) : 歯の長さ [2]	\(\alpha\) : 歯の角度
\(A_\mathrm{t}(l_\mathrm{t}, a_0, a_\mathrm{max}, \alpha)\) : 歯の断面積	\(n_\mathrm{t}\) : 歯の数 [2]
\(\beta\) : plateの貫入角度	\(z\) : 貫入量
\(A_\mathrm{s}\) : 土に貫入しているplateの面積
\(g\) : 重力加速度 [2]	\(\rho\) : 土密度 [2]
\(c_a\) : 土とplate間の粘着力 [2]	\(\mu_{\mathrm{tool}}\) : 土とplate間の摩擦係数 [2]
\(E^{\mathrm{bulk}}\) : 土のヤング率 [2]	\(\nu\) : 土のポアソン比 [2]
\(\phi\) : 内部摩擦角 [2]	\(\psi\) : ダイレイタンシー角 [2]
\(K_0 = 1- \sin \phi\) : 静止土圧係数(Jakyの式)
\(p_\mathrm{t}(E^{\mathrm{bulk}}, \nu, \phi, c_\mathrm{a}, \psi, a_0, a_\mathrm{max})\) : teethに加わる土の圧力

とおいて、次式から貫入抵抗力を求める。

plateにかかる土の垂直圧力 \(p_\mathrm{n}\)

(29)\[\begin{aligned} p_\mathrm{n} = \frac{1}{2} \rho g z [(1 + K_0) + (1 - K_0)\cos(2 \beta)] \end{aligned}\]

plateに加わる力 \(f_\mathrm{ps}\)

(30)\[\begin{split}\begin{aligned} f_\mathrm{ps} = (c_\mathrm{a} + \mu_{\mathrm{tool}} p_\mathrm{n}) A_\mathrm{s} \\ \end{aligned}\end{split}\]

teethに加わる力 \(f_\mathrm{pt}\)

(31)\[\begin{split}\begin{aligned} f_\mathrm{pt} = n_\mathrm{t} [ p_\mathrm{t} + (c_\mathrm{a} + \mu_\mathrm{tool} p_\mathrm{t} / \tan \alpha)] A_\mathrm{t} \\ \end{aligned}\end{split}\]

貫入抵抗力 \(f_\mathrm{p}\)

(32)\[\begin{aligned} -f_\mathrm{ps} \leq f_\mathrm{p} \leq f_\mathrm{ps} + f_\mathrm{pt} \end{aligned}\]

\(p_\mathrm{t}\) はcavity expansion theory (空洞膨張論)に基づいて計算する。 詳細は [agxTerrainReport2019] を参照されたい。

破壊領域 Active zone

• Excavation Model — AGX Dynamics documentation

agxTerrainでは土くさびを内包する破壊領域をacitive zoneとよぶ。 Active zoneは内部摩擦角 \(\phi\)、plateの貫入角度 \(\beta\)、failure angle(破壊角度) \(\theta\) から成る領域である。

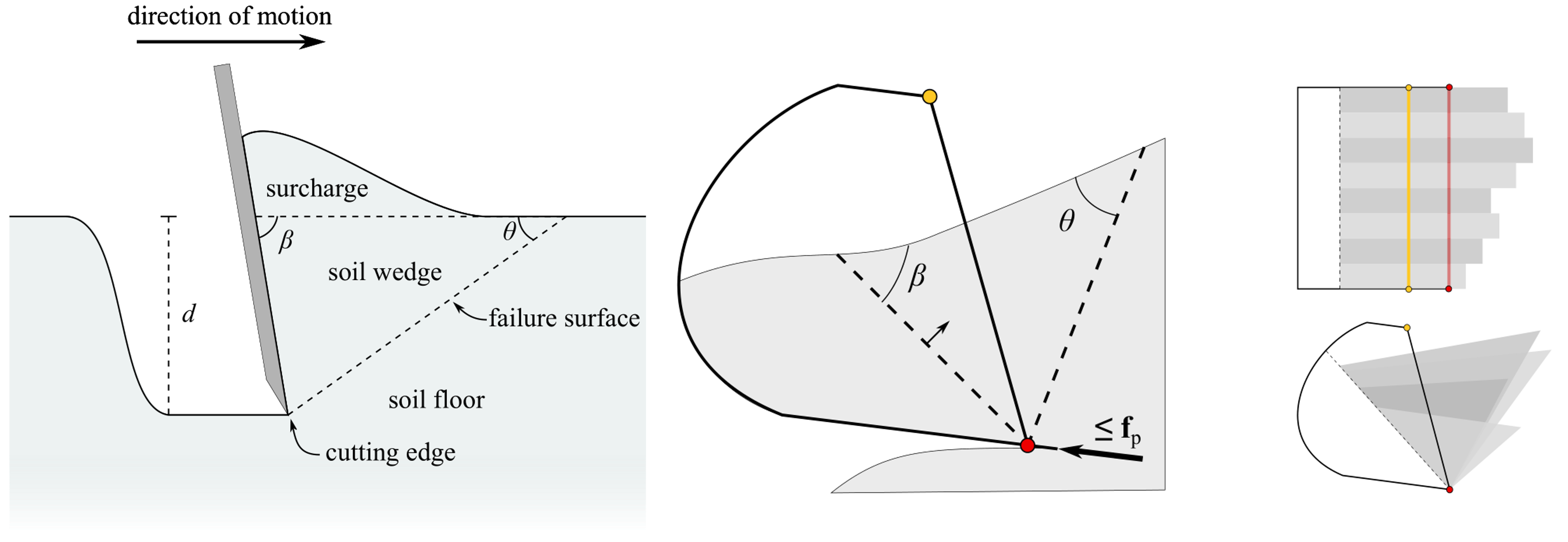
Failure angle \(\theta\) は

(33)\[\theta(\phi, \beta) = \frac{\pi}{2} - \left( \frac{\phi + \beta}{2} \right)\]

である。plateの貫入角 \(\beta\) はバケット内の土量に応じて変化するsecondary separation plateの姿勢から決まる。

Secondary separation plateの姿勢は ショベルの形状を定義するベクトルが成す面法線と ショベルに流入する土の割合から求める。 ショベルの形状を定義するベクトルは、

• CuttingDirection: 底面と平行な掘削方向

• CuttingEdge: 底面の先端

• TopEdge: 上端

であり、それぞれのベクトルが成す面法線は

• CuttingDirectionとCuttingEdgeが成す面法線

• CuttingEdgeとTopEdgeが成す面法線

である。これらの面法線とdeadload(ショベルに流入する土の割合)で補間した面がsecondary separation plateである。

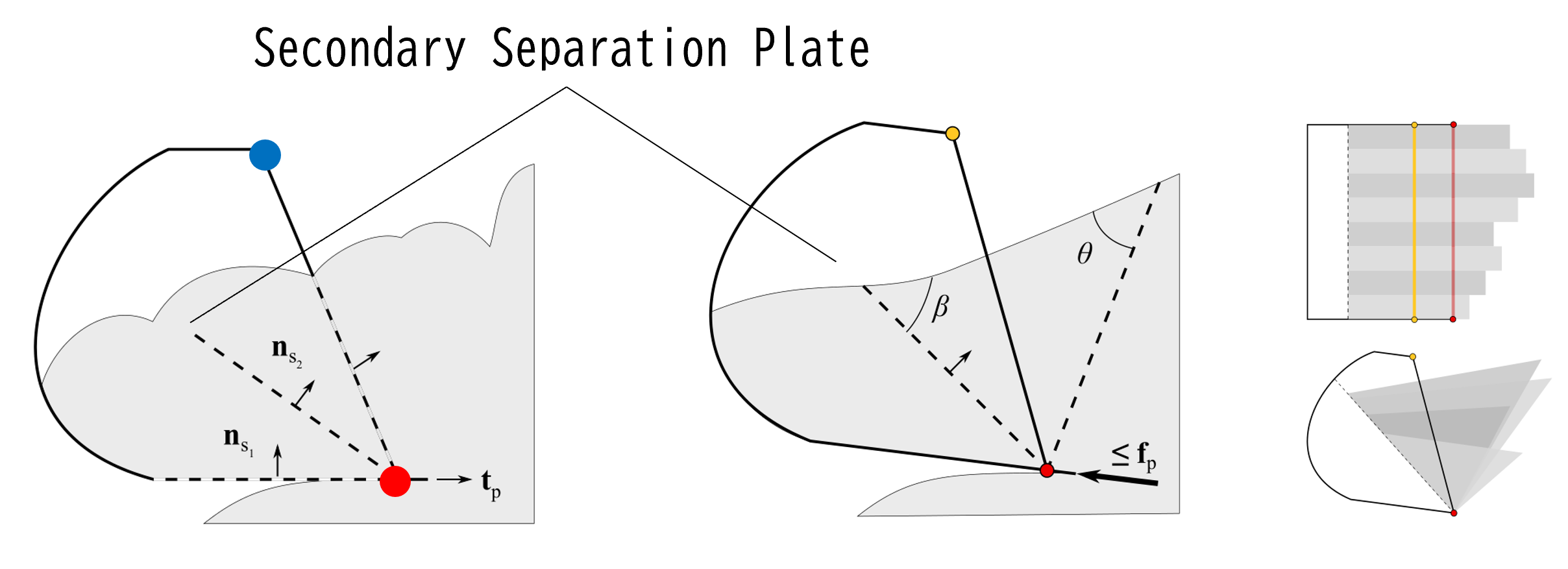
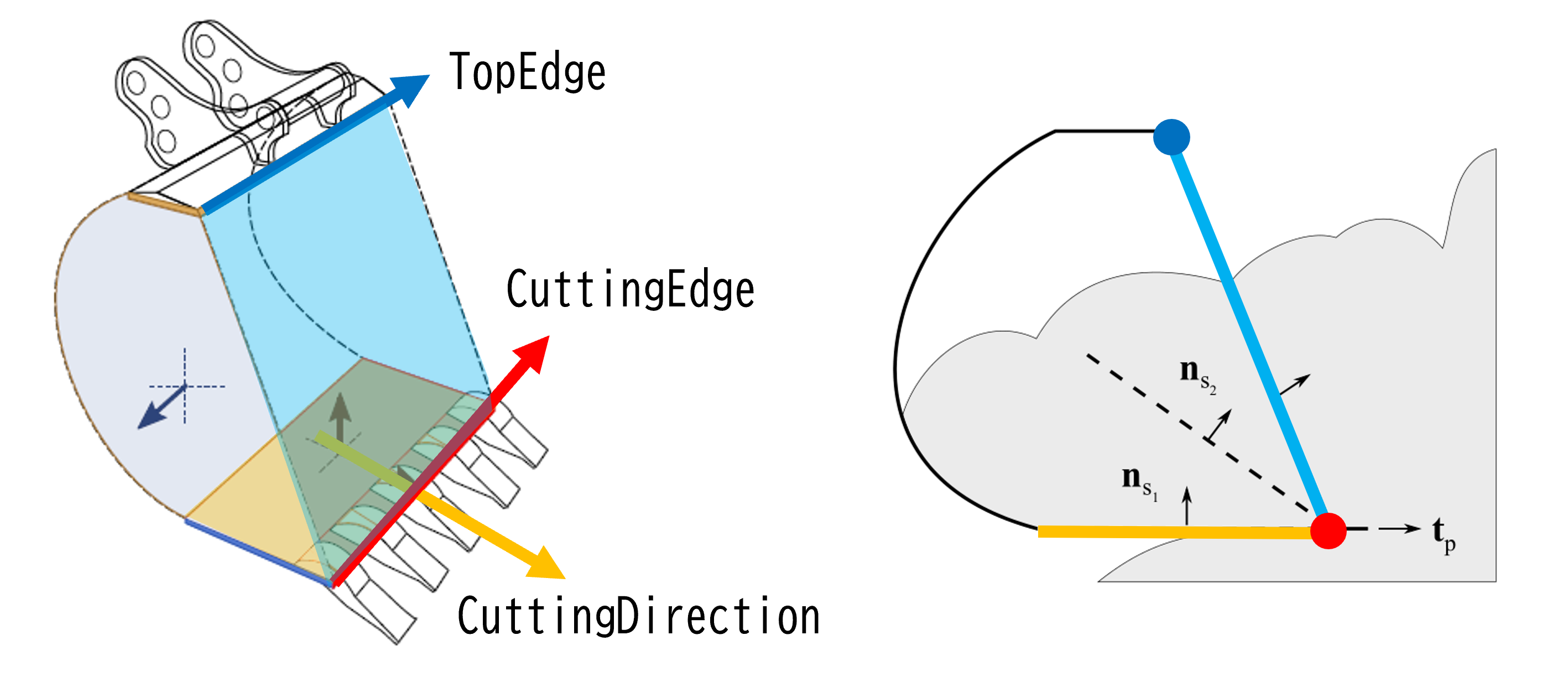
Active zoneの実例

内部摩擦角 \(\phi=23 \mathrm{deg}\) として、Full NDEMシミュレーションを行い、 貫入角度とfailure angleを取得した。 内部摩擦角とシミュレーションで得た貫入角度をfailure angleの 式(33) に代入し、failure angleを推定した。 下表のとおり、Full NDEMとfailure angleの計算式の値は逸脱していなかった。

	failure angle \(\theta\) (deg)	貫入角度 \(\beta\) (deg)
Full NDEMの結果	34 - 40	90
failure angleの計算式	34

補足: 土密度と応力の関係式の導出

式(21) の間隙比 \(e_\mathrm{cpt}\) と応力 \(\sigma_\mathrm{cpt}\) を最新の \(e_{k+1}\) と \(\sigma_\mathrm{k+1}\) に置き換えて、式変形する。

(34)\[\begin{split}\begin{aligned} C_\mathrm{c} &= \frac{e_\mathrm{b} - e_{k+1}}{\ln(\sigma_{k+1}/\sigma_\mathrm{b})} \\ e_\mathrm{b} - e_{k+1} &= C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_\mathrm{b}} \right) \\ \left( \frac{\rho_s}{\rho_\mathrm{b}} -1 \right) - \left( \frac{\rho_s}{\rho_{k+1}} - 1 \right) &= C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_b} \right) \\ \frac{\rho_s}{\rho_{k+1}} &= \frac{\rho_s}{\rho_\mathrm{b}} - C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_b} \right) \\ \rho_{k+1} &= \rho_s \left[ \frac{\rho_s}{\rho_\mathrm{b}} - C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_b} \right) \right]^{-1} \\ \end{aligned}\end{split}\]

ここで、体積分率 \(\varphi_\mathrm{b} = \rho_\mathrm{b} / \rho_s\) を導入すると、

(35)\[\begin{split}\begin{aligned} \rho_{k+1} &= \rho_s \left[ \varphi_\mathrm{b}^{-1} - C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_b} \right) \right]^{-1} \\ \rho_{k+1} &= \varphi_\mathrm{b} \rho_s \left[ 1 - \varphi_\mathrm{b} C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_b} \right) \right]^{-1} \\ \rho_{k+1} &= \rho_\mathrm{b} \left[ 1 - \varphi_\mathrm{b} C_\mathrm{c} \ln \left(\frac{\sigma_{k+1}}{\sigma_b} \right) \right]^{-1} \\ \end{aligned}\end{split}\]

となる。

[1]

日本の土質力学の教科書では \(\log_{10}\) が主流のようだが、agxTerrainでは \(\ln\)、\(\log_{e}\) である。

[2] (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22)

ユーザが設定可能なパラメータ。