ボクセルモデル

ボクセルモデルの定義

• Terrain Grid Structure — AGX Dynamics documentation

連続体である土をシミュレーションできる形に空間離散化する。 離散化にはボクセル格子(立方体格子)を使う。 各ボクセルには土が充填され、土の圧縮に応じて、ボクセル毎に土の密度が変動する。

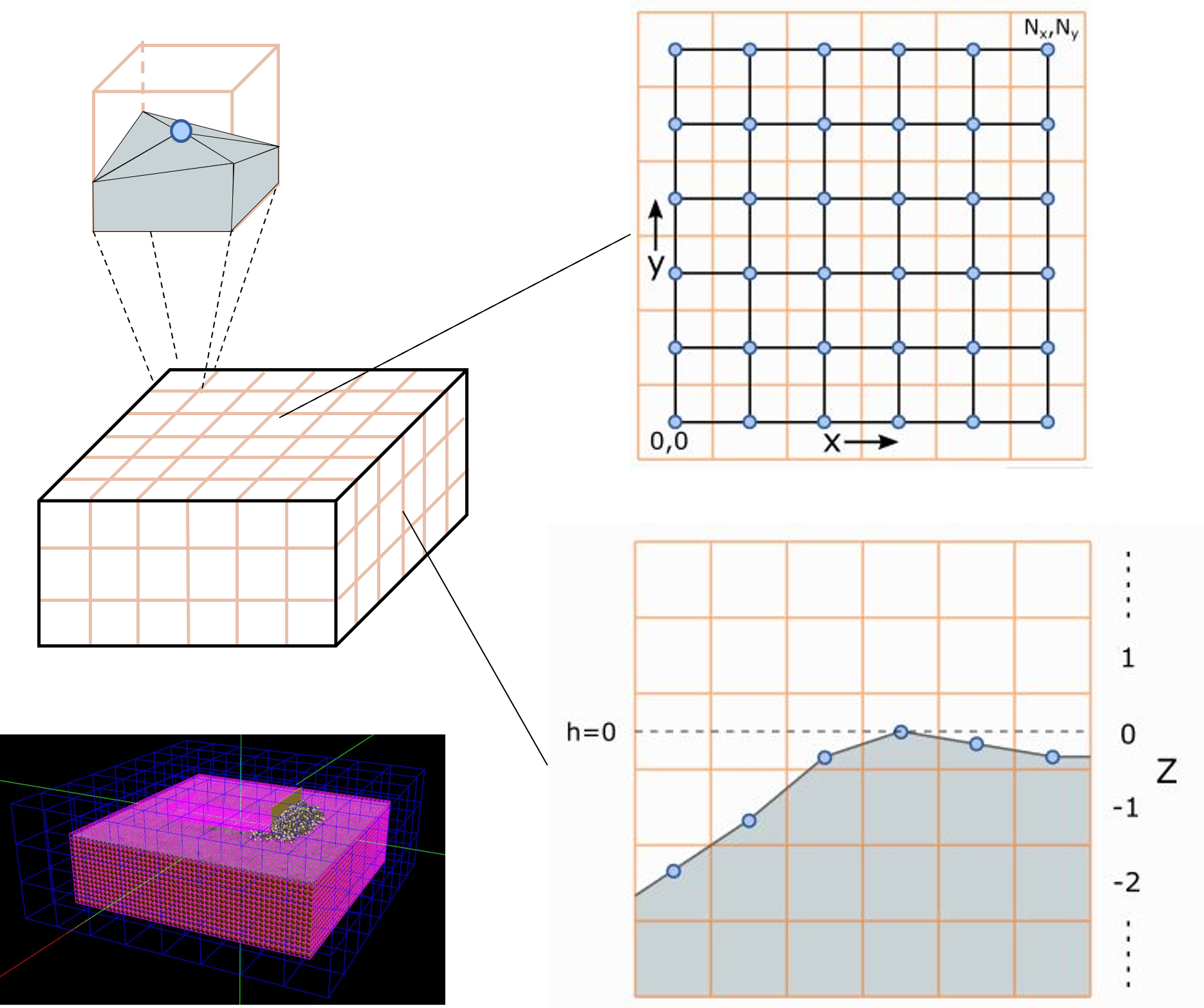
ボクセルモデルの定義を次に示す。

\(l_0\)	ボクセルの辺長
\(V_0 = {l_0}^{3}\)	ボクセルの体積
\(\bm{i} = (i, j, k)\)	ボクセルのインデックス。 \(i\) : x方向i番目、\(j\) : y方向j番目、\(k\) : z方向k番目。
\(\bm{i^\prime} = (i, j, k^\prime)\)	空でないz方向トップのボクセルのインデックス
\(k^\prime\)	空でないz方向のトップインデックス
\(z_\bm{i^\prime}\)	ボクセル \(\bm{i^\prime}\) のz座標値。\(k^\prime=0\) のとき、 \(z = -\frac{1}{2} l_0\)。\(k^\prime=1\) のとき、 \(z = \frac{1}{2} l_0\)。
\(V_\bm{i}\)	ボクセル \(\bm{i}\) の土体積
\(\varphi_\bm{i} = V_\bm{i} / V_0 \in [0, 1]\)	ボクセル \(\bm{i}\) の土体積占有率(solid occupancy)。\(\varphi_\bm{i} = 1\) はボクセルに土が完全に満たされている状態。
\(\rho_\bm{i}^\mathrm{solid} \in [\rho_\mathrm{max}, \rho_\mathrm{min} ]\)	ボクセル \(\bm{i}\) の土密度
\(w_\bm{i} = \rho_\bm{i}^\mathrm{solid} / \rho_0\)	ボクセル \(\bm{i}\) の土の圧縮レベル(compaction level)
\(m_\bm{i} = \rho_\bm{i}^\mathrm{solid} V_\bm{i}\)	ボクセル \(\bm{i}\) の土質量

ボクセルに加わる応力

• Soil Compaction — AGX Dynamics documentation

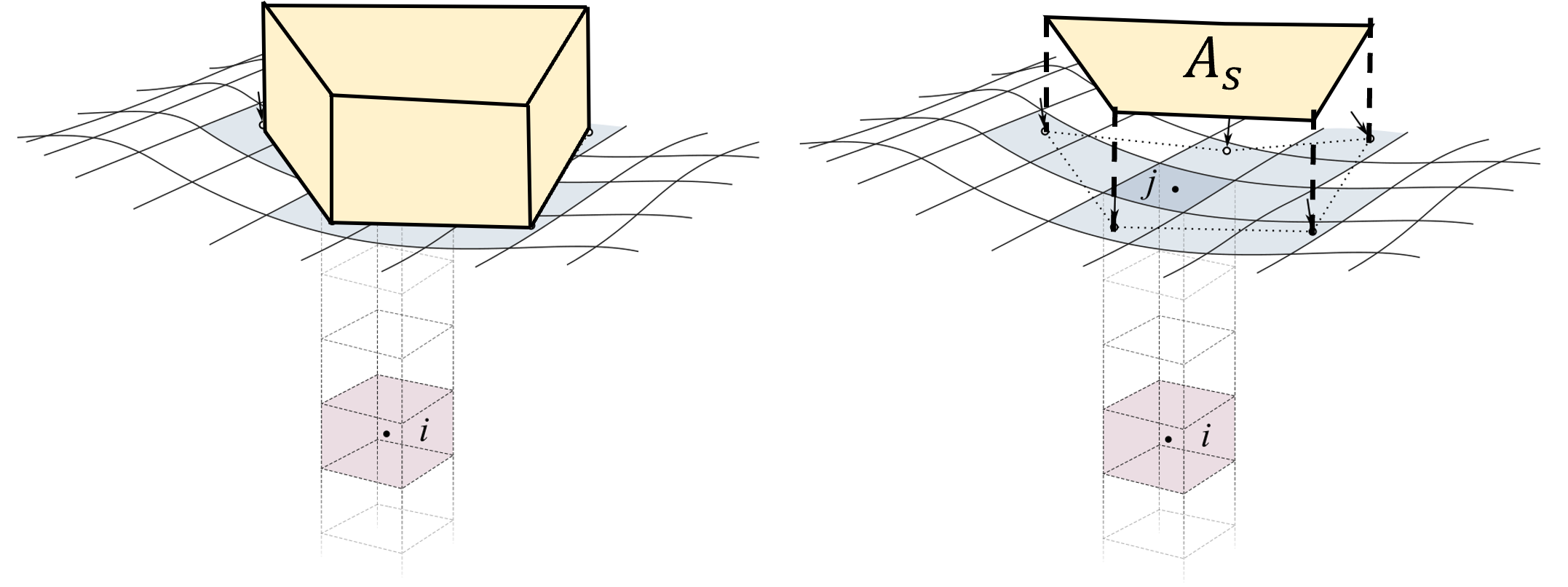
土の圧縮 計算に使う応力を計算する。 応力はテレインに加わる荷重を各ボクセルに加わる応力に変換して求める。

ボクセルに跨るように物体を接触させて荷重をかけ、接触点を包含する領域を接触領域とする。 ここで、

\(f_\mathrm{s}\) : 接触領域にかける荷重

\(A_\mathrm{s}\) : 接触領域にかかるボクセルの合計面積。接触領域の面積の近似。

とおいて、次式から応力を求める。

接触領域内のボクセル \(\bm{j}\) に加わる応力

(36)\[\sigma_\bm{j}^\mathrm{s} = \frac{f_\mathrm{s}}{A_\mathrm{s}}\]

ボクセル \(\bm{i}\) に加わる応力

(37)\[\sigma_\bm{i}^\mathrm{v} \left( z_\bm{i}, \sigma_\bm{j}^\mathrm{s}, A_\mathrm{s} \right) = \sigma_\bm{j}^\mathrm{s} \left[ 1 - \left( \frac{z_\bm{i}}{\sqrt{A_\mathrm{s} + z_\bm{i}^2}} \right)^3 \right]\]

ボクセルモデルから粒子モデルへの変換

• Mass deformation model — AGX Dynamics documentation

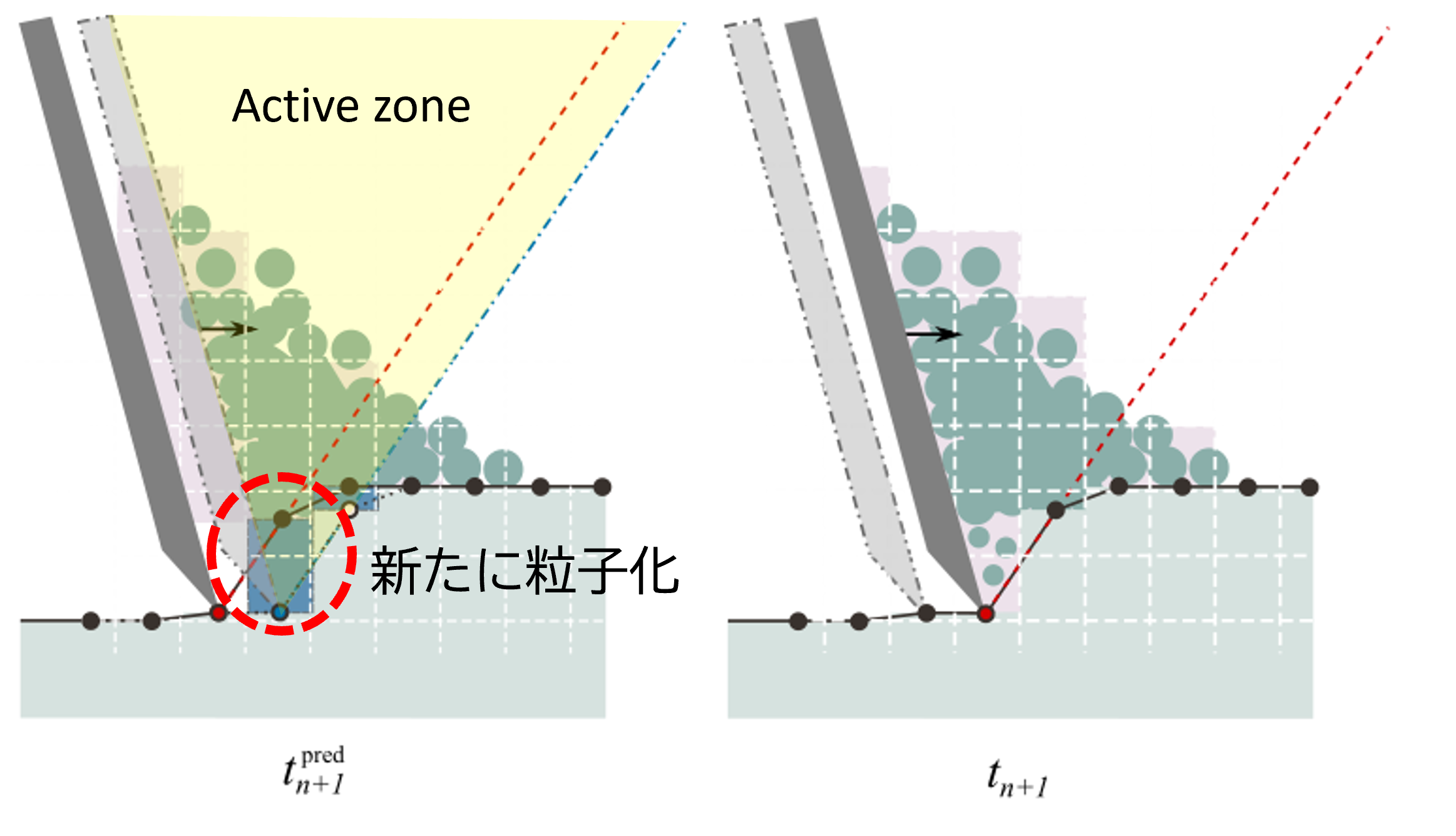
ショベルがテレインに貫入すると active zone が形成される。 agxTerrainは次の手順でactive zone内にある土が充填されたボクセルを粒子モデルに変換する。

Active zoneと重複する粒子化対象のボクセルを列挙し、ボクセル毎に粒子化をする。 ボクセル \(\bm{i}\) の土体積のうち、粒子化させる土体積(流動質量化させる体積, fluidized volume) \(\Delta V_\bm{i}^\mathrm{fluid}\) を求める。 そして、土密度 \(\rho_\bm{i}^\mathrm{solid}\) から、粒子化させる質量(流動質量, fluidized mass)を求める。

ボクセル \(\bm{i}\) の流動質量 fluidized mass

(38)\[m_\bm{i}^\mathrm{fluid} = \rho_\bm{i}^\mathrm{solid} \Delta V_\bm{i}^\mathrm{fluid}\]

流動質量を 流動質量の配分ルール に基づいて、新粒子の生成、新粒子への追加、残余流動質量に分配する。 したがって、全ての流動質量が粒子になるとは限らない。

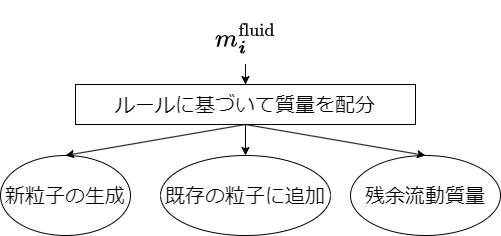
残余流動質量はボクセルに戻す。 残余流動質量を体積 \(\Delta V_\bm{i}^\mathrm{residual}\) に変換し、ボクセルの土体積占有率を更新する。

ボクセル \(\bm{i}\) の土体積占有率の更新

(39)\[\varphi_\bm{i} = \frac{\Delta V_\bm{i}^\mathrm{solid} - \Delta V_\bm{i}^\mathrm{fluid} + \Delta V_\bm{i}^\mathrm{residual} }{V_0}\]

最後に、次式でテレインの表面高さを更新する。

テレインの表面高さの更新

\(h_{ij} = z_\bm{i^\prime} + ( \varphi_\bm{i^\prime} - 1/2 ) l_0\)

流動質量の配分ルール

流動質量の配分は次のルールにしたがう。

ボクセルモデル→粒子モデルへの変換

• 流動質量を新粒子の生成、既存の粒子に配分する

• 土ほぐしによる土量と密度の更新 により、粒子の体積を膨張させる

• 粒子半径のサイズを \(d \in [d_\mathrm{min}, d_\mathrm{max}]\) に制限する

• 粒子の成長速度を \(\dot{d} \leq \dot{d}_\mathrm{max}\) に制限する

• 粒子同士の質量の受け渡しは \(3 \times 3 \times 3\) のボクセルの範囲に制限する

• 質量保存を保ちながら、質量を配分する

• Active zone外に残余流動質量があるときは直下のボクセルに戻す

• Active zone内に残余流動質量があるときは、粒子速度で別のボクセルに移動する

• 残余流動質量を戻すボクセルの密度が上限 \(\rho_\mathrm{max}\) に達している場合は、一つ上のボクセル戻す

粒子モデル→ボクセルモデルへの変換

• Active zone外にある粒子の質量は接触速度、active zoneとの距離、条件の継続時間に応じて、接しているボクセルに戻す

• 質量をボクセルに戻す時にも 土ほぐしによる土量と密度の更新 を適用する

表層すべり: テレインの平衡化 Terrain equilibration

• Angle of Repose — AGX Dynamics documentation

土を積み上げると土の表面がすべり、平衡状態に落ち着く。 agxTerrainは摩擦角を安息角の基準とし、圧縮レベルに応じてすべり出しの角度を決めて、表層すべりを表現する。 そして、表層すべりにより変化するテレインの高さを更新する。

表層すべりによるテレインの高さの更新は、

\(l_0\) : ボクセルの辺長

\(M\) : 土の圧縮による影響を指数関数的に安息角に与える定数

\(w_\bm{i}\) : ボクセル \(\bm{i}\) における土の圧縮レベル

\(S_\mathrm{f}\) : 土量変化率

とおき、次の手順で表現する。

1. 摩擦角 \(\phi\) を安息角として、相対高さ \(h_\mathrm{r}\) を求める。

(40)\[h_\mathrm{r} = l_0 \tan \phi\]

2. 土の圧縮の影響を \(h_\mathrm{r}\) に加える。

(41)\[\begin{split}\begin{aligned} m &= 2^{M \{w_\bm{i} - 1.0 / S_\mathrm{f} \}} \\ h_\mathrm{r} &= h_\mathrm{r} m \end{aligned}\end{split}\]

3. 隣り合うボクセルの相対高さが \(h_\mathrm{r}\) となるように質量の受け渡しをする。

4. 1-3を全てのボクセルについて繰り返し処理する。

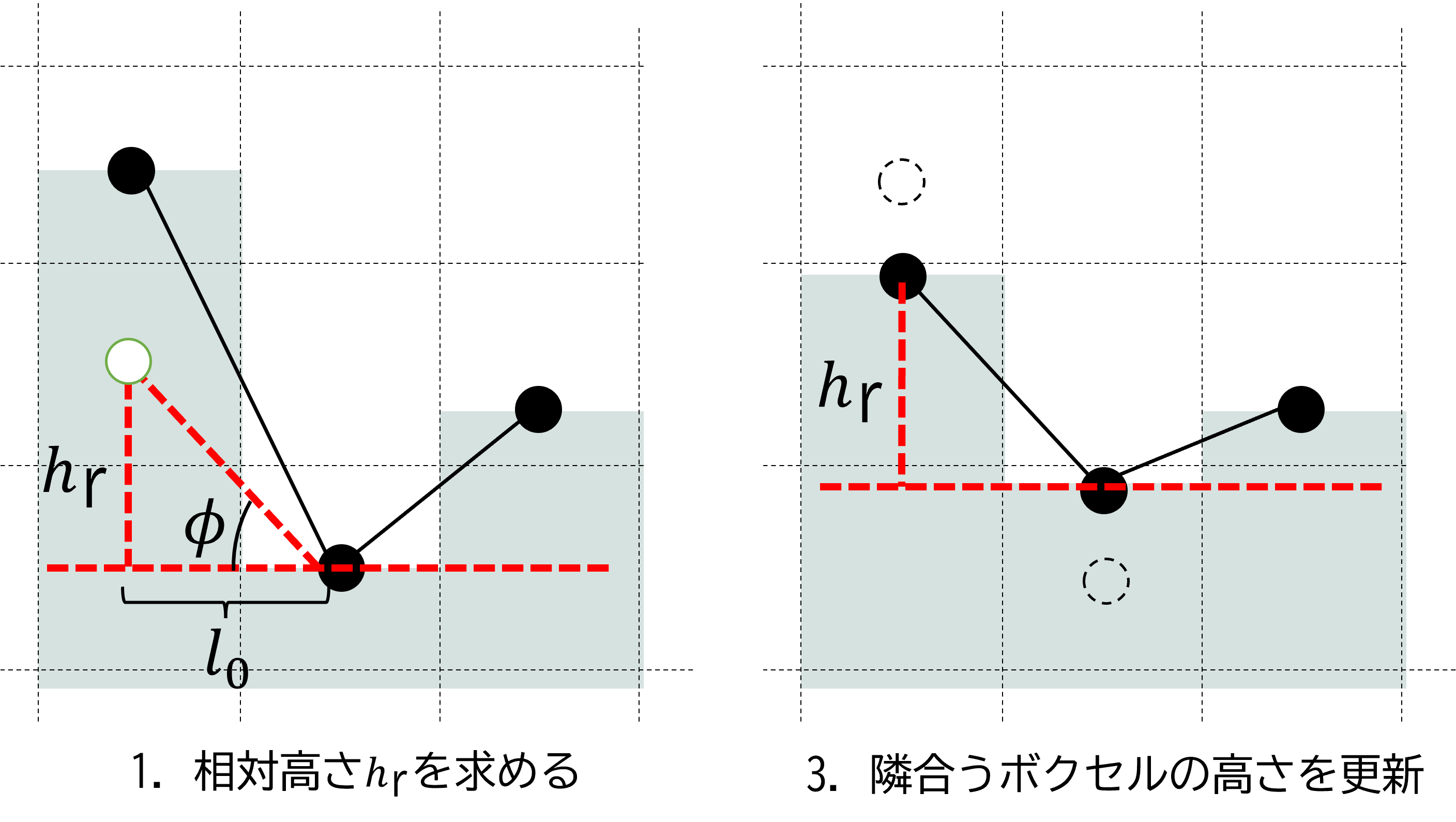
高さの計算例

\(M=1.0\)、\(S_\mathrm{f}=1.0\) とする。

• \(w_\bm{i} = 0.5\) のとき、\(h_\mathrm{r} = 0.71 h_\mathrm{r}\)

  • 圧縮レベルが低いと滑りやすく、相対高さが低くなる

• \(w_\bm{i} = 1.0\) のとき、\(h_\mathrm{r} = 1.0 h_\mathrm{r}\)

  • 圧縮レベルが原位置と同じになる

• \(w_\bm{i} = 1.5\) のとき、\(h_\mathrm{r} = 1.5 h_\mathrm{r}\)

  • 圧縮レベルが高いと滑りにくく、相対高さが高くなる