粒子モデル

粒子モデルの概要

• Dynamic Soil — AGX Dynamics documentation

• AGX Granular — AGX Dynamics documentation

粒子モデルは土の移動を表すモデルである。 agxTerrainは粒子の運動計算にNDEM(Nonsmooth discrete element method)を使う。 接触拘束には 非線形Hertz-Mindlin接触モデル を使い、

• 粒子同士の接触

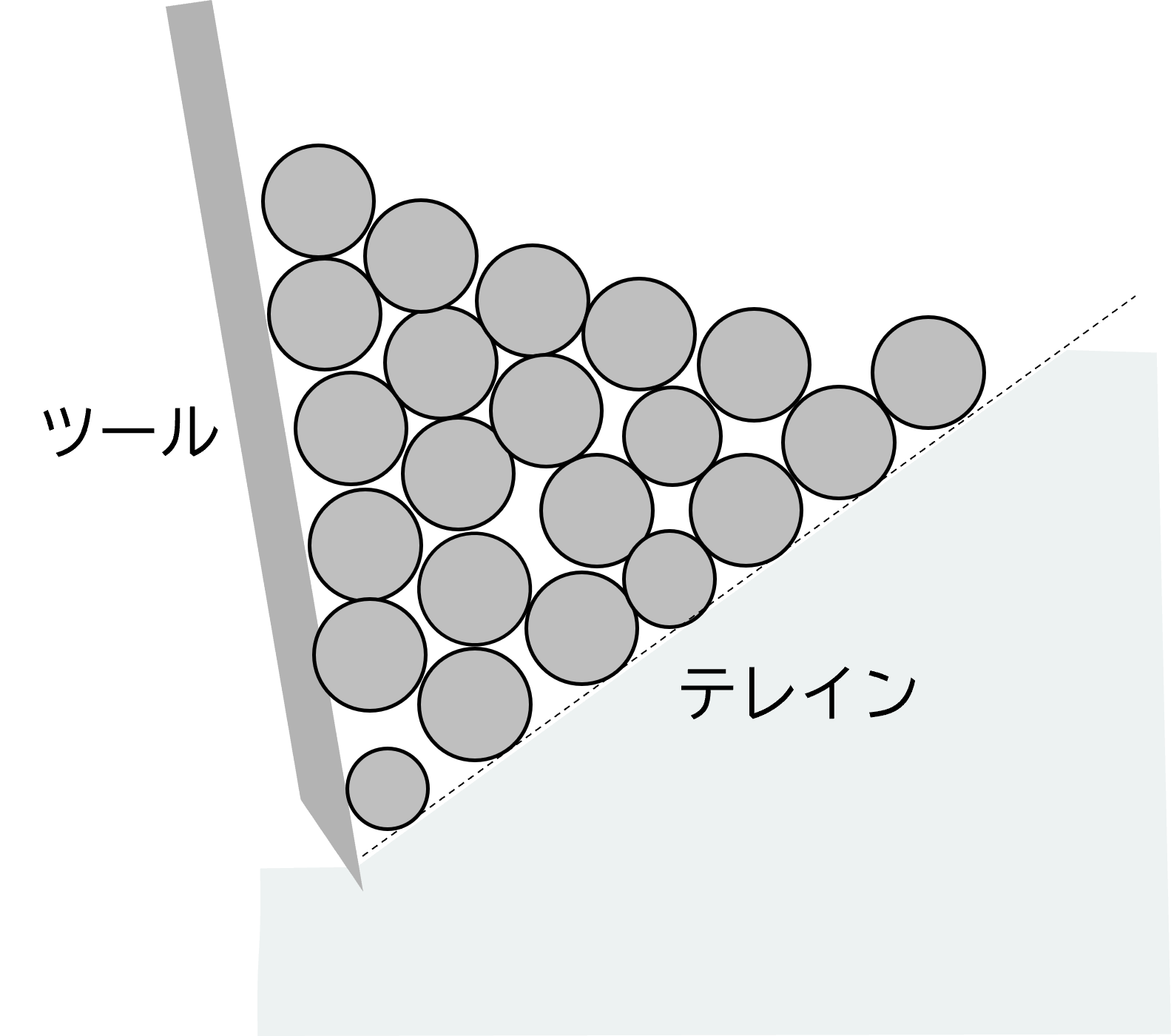
• 粒子と接触するショベルとテレイン: 粒子から受ける接触力に左右されないキネマティックな壁(境界条件)

を拘束条件とし、微分代数方程式を離散化した SPOOK に帰着させる。 拘束はドメイン分割による並列計算とウォームスタート [Wang2016] を実装した反復法ソルバ PPGS(Parallel projected Gauss-Seidel solver) を使って解く。

非線形Hertz-Mindlin接触モデル

接触の計算に非線形Hertz-Mindlin接触モデルを使う。 接触は

\(\delta\) : 粒子の侵入量	\(\dot{\delta}\) : 粒子の相対侵入速度
\(\bm{n}\) : 抗力方向ベクトル	\(\eta\) : 材料粘性定数
\(d_\mathrm{a}\) 粒子aの直径	\(d_\mathrm{b}\) 粒子bの直径
\(d^* = (d_\mathrm{a}^{-1} + d_\mathrm{b}^{-1})^{-1}\) : 有効直径	\(d\) 粒子の直径
\(E_\mathrm{p}\) : 粒子間のヤング率 [1]	\(\nu_\mathrm{p}\) : 粒子のポアソン比
\(\mu_\mathrm{p}\) : 粒子間の摩擦係数 [1]	\(\mu_\mathrm{pr}\) : 粒子間の転がり抵抗係数 [1]
\(e_\mathrm{p}\) : 粒子間の反発係数 [1]

とおいて、次式で計算する。

バネ係数

(42)\[k_\mathrm{n} = \frac{E_\mathrm{p} \sqrt{2d^*}}{3(1 - \nu_\mathrm{p}^2)}\]

粘性係数

(43)\[c_\mathrm{d} = \frac{4(1 - \nu_\mathrm{p}^2)(1 - 2\nu_\mathrm{p})\eta}{15E_\mathrm{p} \nu_\mathrm{p}^2}\]

粒子間の接触抗力

(44)\[\bm{f}_\mathrm{n} = k_\mathrm{n} \delta^\frac{3}{2} \bm{n} + k_\mathrm{n} c_\mathrm{d} \delta^\frac{1}{2} \dot{\delta} \bm{n}\]

※ 衝突時は反発係数 \(e_\mathrm{p}\) を使い、速度変化させる。

粒子間の接線力(摩擦力)

(45)\[f_t \leq \mu_p |\bm{f}_\mathrm{n}|\]

粒子間の転がり抵抗力

(46)\[\tau_\mathrm{r} \leq \mu_\mathrm{pr} \left(\frac{d}{2}\right) |\bm{f}_\mathrm{n}|\]

粒子-テレイン、粒子-オブジェクト(ショベルなど)との接触についても同じ計算式を使う。 それぞれのパラメータを次に示す。

	粒子-テレイン	粒子-オブジェクト
ヤング率	\(E_\mathrm{pt}\) [1]	\(E_\mathrm{po}\) [1]
摩擦係数	\(\mu_\mathrm{pt}\) [1]	\(\mu_\mathrm{po}\) [1]
転がり抵抗係数	\(\mu_\mathrm{ptr}\) [1]	\(\mu_\mathrm{por}\) [1]
反発係数	\(e_\mathrm{pt}\) [1]	\(e_\mathrm{po}\) [1]

[1] (1,2,3,4,5,6,7,8,9,10,11,12)

ユーザが設定できるパラメータ。