拘束ソルバ

  • AGXはハイブリッドソルバ(Hybrid solver)。拘束条件毎にソルバを指定できる。

    • 直接法(Direct solver): 計算精度高い

    • 反復法(Iterative solver): 大量の接触拘束を解くことに適する

    • スプリット(Split solver): 接触専用。直接法で抗力を解き、反復法で抗力と摩擦を解く。

  • 参考文献

概要

../../../../_images/solver_overview.png

拘束ソルバは 時間積分スキーム SPOOK ( 式(15) )について、拘束条件を満足するための \(v_{k+1}\) と \(\lambda_{k+1}\) を求める。 拘束条件には等式、不等式拘束が含まれており、MLCP(Mixed Linear Complementarity Problem、混合線形相補性問題)を解く。

速度の更新(ホロノミック拘束のみ版)

(15)\[\begin{split}\left[\begin{array}{cc} \bm{M} & -\bm{G}_k^T \\ \bm{G}_k & \bm{\Sigma} \end{array}\right]\left[\begin{array}{c} \bm{v}_{k+1} \\ \bm{\lambda_{k+1}} \end{array}\right]=\left[\begin{array}{c} \bm{M} \bm{v}_k+h \bm{f}_k \\ -\frac{4}{h} \bm{\gamma} \bm{g}_k+\bm{\gamma} \bm{G}_k \bm{v}_k \end{array}\right]\end{split}\]

位置の更新

(16)\[\bm{x}_{k+1} = \bm{x}_k + h \bm{v}_{k+1}\]

AGXの拘束ソルバ

AGXには複数の拘束ソルバがある。それぞれの特徴を次に示す。

直接法(Direct solver)

  • ガウスの消去法のように、行列の入れ替え操作で解くタイプ

  • Block sparse LDLT factorization + Block pivoting method

  • AGXのジョイントソルバのデフォルト

  • 機械精度

  • 大きい質量比に強い

  • 大量の接触には向いていない

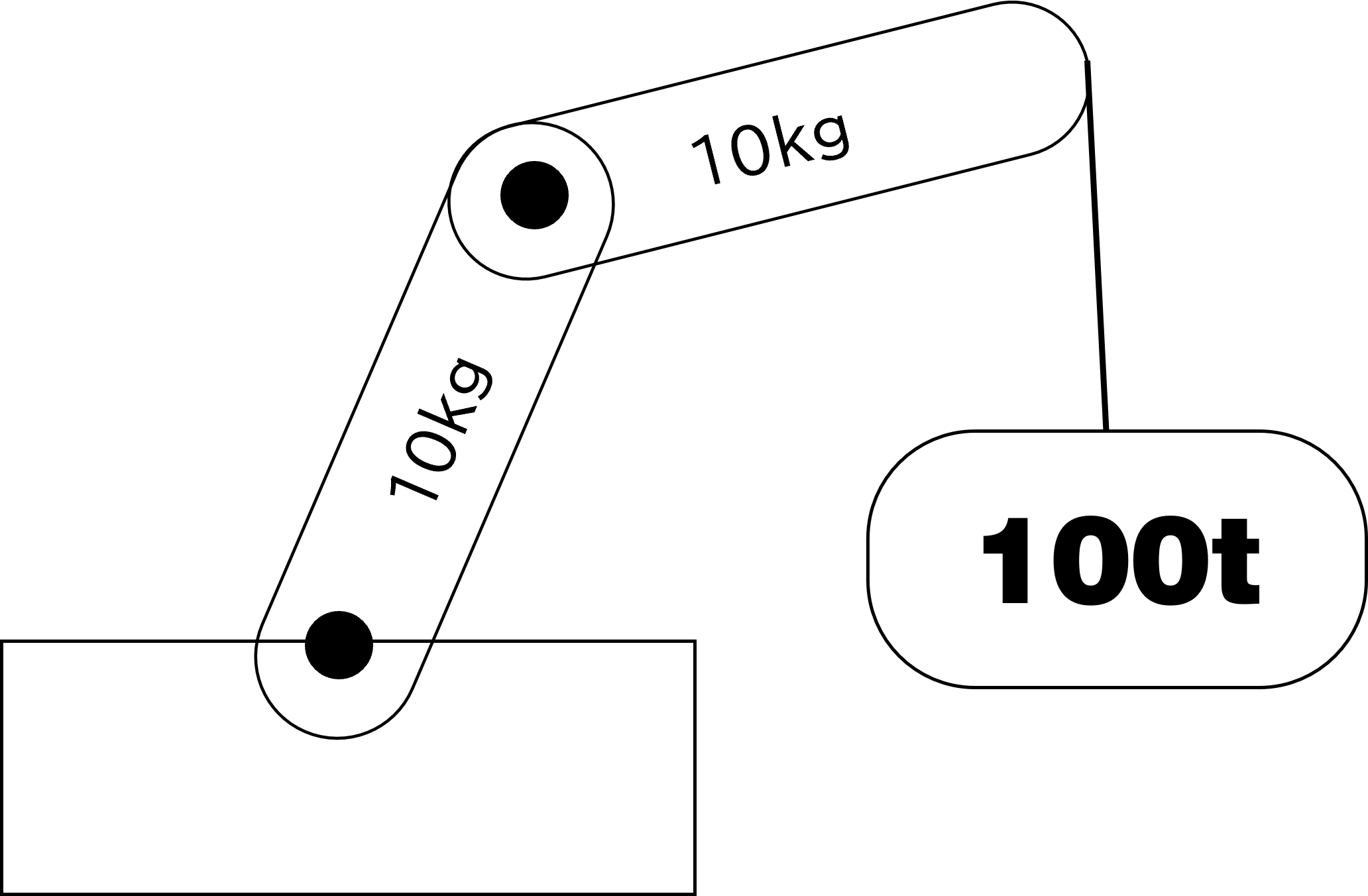
../../../../_images/solver_mass_ratio.png

反復法(Iterative solver)

  • 漸化式の形にして収束計算をするタイプ

    • \(x_i^{k+1} = f_i(\bm{x}^k)\) 。\(i\) : \(i\) 番目の行、\(k\) : 反復回数、\(f_i(\bm{x}^k)\) : \(x_i^{k+1}\) を求める関数。

  • Projected Gauss-Seidel + 並列計算

  • 適当な反復回数で計算を打ち切るので精度は低い

  • 大量の接触を扱うのに向いている

スプリット(Split solver)

  • 接触拘束専用

  • AGXの接触ソルバのデフォルト

  • 直接法で抗力(法線方向)を求め、その結果を使って反復法で抗力と摩擦力(接線方向)を求める

ソルバの指定

AGXは接触、ジョイント毎にソルバを指定できる。 例えば次図のように、精度と速度を調整できる。

ロボットハンドと把持対象:

きっちりと摩擦を効かせて把持できるように直接法を指定

床と物:

全体の計算量を抑えるために反復法を指定

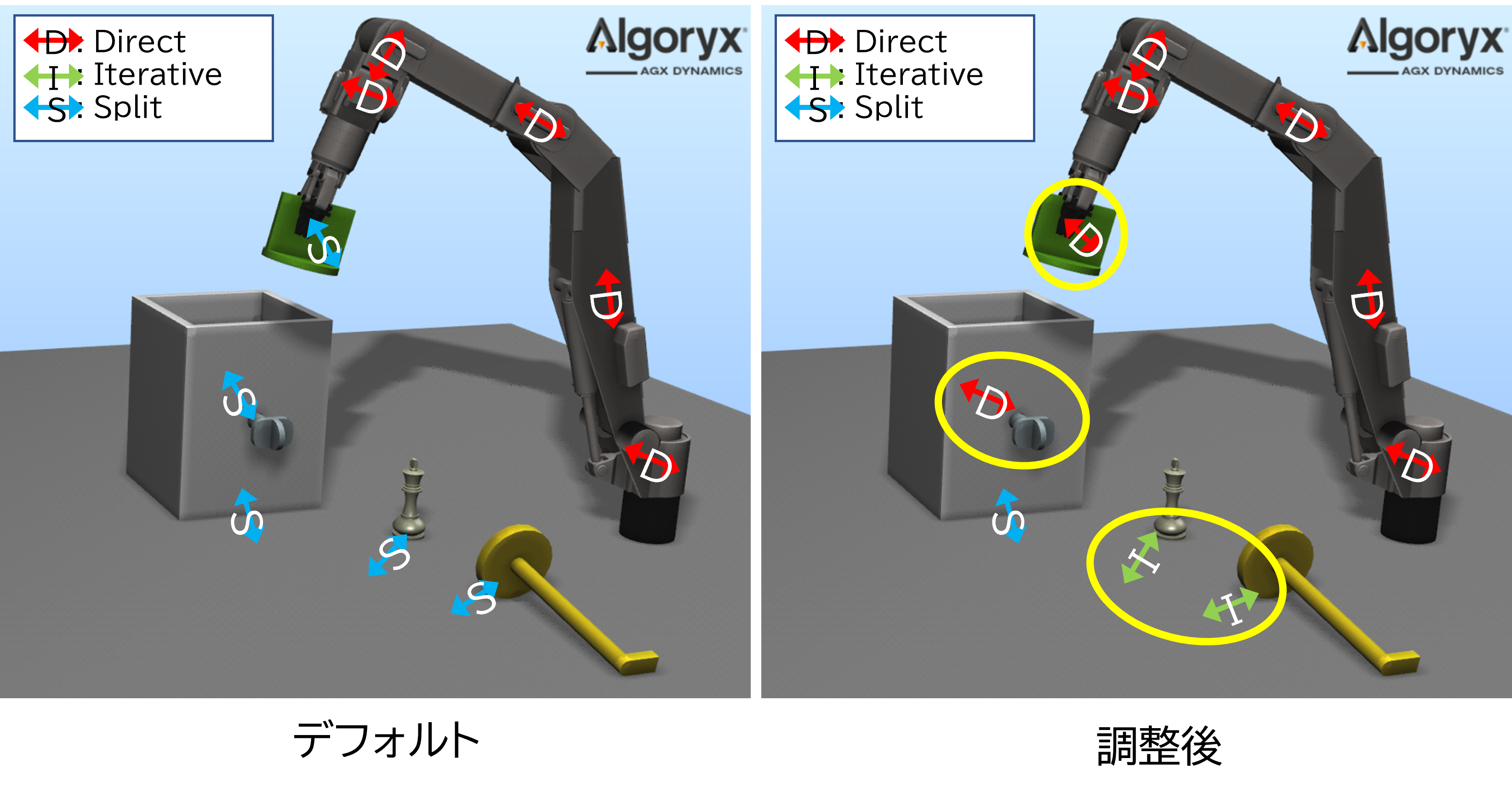
../../../../_images/solver_hybrid.png

直接法と反復法の精度と計算時間の比較

剛体棒をシミュレーションし、直接法と反復法の精度と計算時間を比較した。

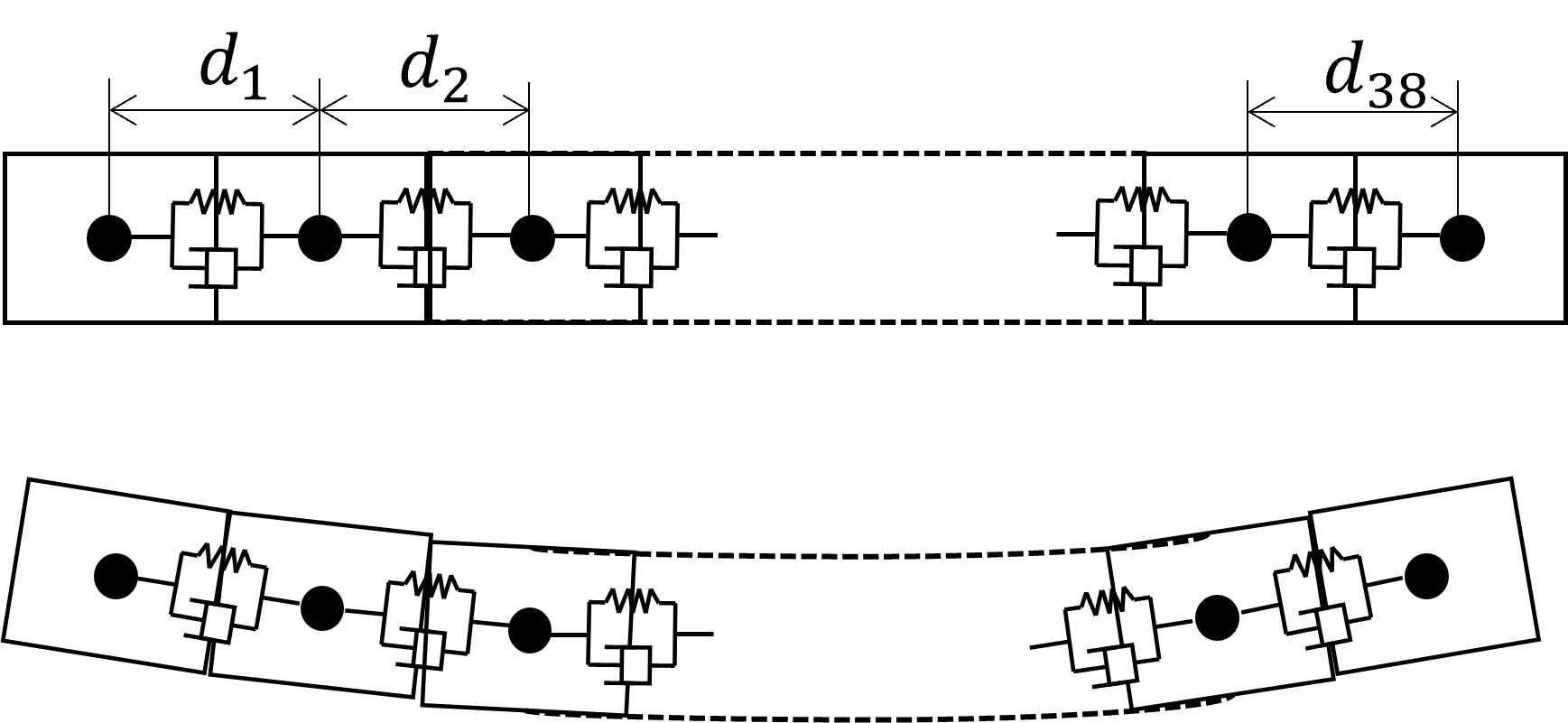
../../../../_images/solver_beam.png

シミュレーションの条件を次に示す。

  • 2s間のシミュレーション

  • 複数のBox間を6自由度拘束(LockJoint)

  • \(n = 39\) : Box数

  • \(m = 1.25 \rm{\,kg}\) : Boxの質量

  • \(d_c = 0.1 \rm{\,m}\) : Box間の初期距離

  • \(k = 1 \times 10^9 \rm{\,N/m}\) : ジョイントの弾性係数

  • \(c = 2 \times 10^9 \rm{\,Ns/m}\) : ジョイントの減衰係数

  • \(\epsilon = 1/k = 1 \times 10^{-9} \rm{\,m/N}\) : ジョイントのコンプライアンス

  • \(\tau = c \epsilon = 2\rm{\,s}\) : ジョイントのスプークダンパ

直接法と反復法について、次の値を取得した。 反復法は反復回数とタイムステップを変更した場合についても取得した。

  • 各Box要素間のずれの合計: \(error = \sum_i (|d_i - d_{c}|)\)。 \(error=0\) が変形なしの真の剛体。

  • 計算時間: 2s以内であればリアルタイム

結果を 表 1 に示す。

表 1 剛体棒のシミュレーション結果

ソルバ

直接法

反復法

反復法

反復法

タイムステップ(s)

0.01667

0.01667

0.01667

0.001

反復回数

数十

10万

10万

\(error\) (m)

1.29E-14

1E-2 - 1E-1

2.14E-5

1.69E-7

計算時間(s)

0.064

2以内
95.101
(約1分半)
1595.6
(約27分)

リアルタイム?

o

o

x

x

直接法は反復法に比べて \(error\) = 1.29E-14 と小さく 機械精度 、計算時間も短い。 反復法はタイムステップを小さくすると、\(error\) が小さくなり精度が向上するが、計算時間が増加する。 反復回数を増やすことでも同様。 反復回数を調整しても、直接法と同等の精度を得るのは難しい。

警告

このケースでは直接法が有効。シミュレーションの内容(解く行列の形)によって結果は異なる。

注釈

  • 炭素原子のサイズは \(70 \rm{\,pm} = 7 \times 10^{-13}\)

  • 倍精度浮動小数点(double)で扱える桁数は約16桁